A Probabilistic Interpretation of Sampling Theory of Graph Signals
Paper and Code
Mar 23, 2015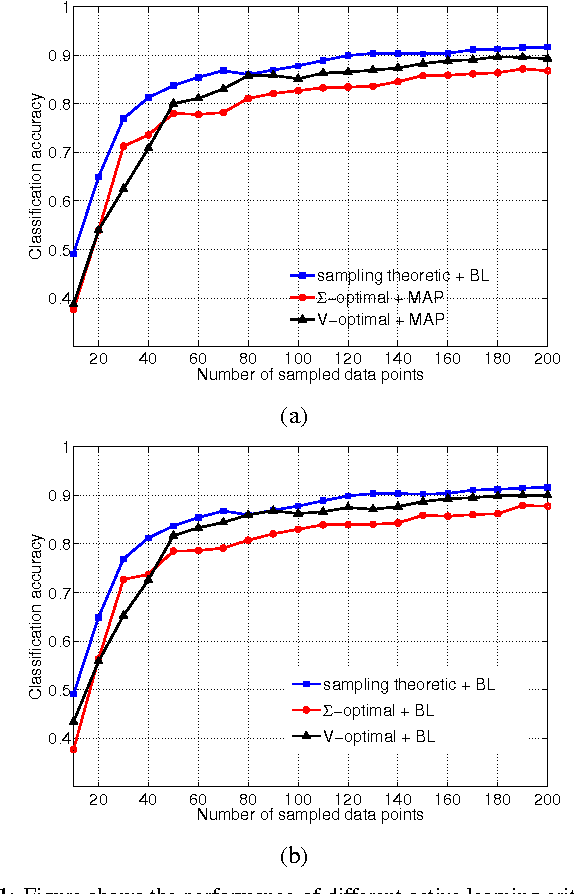
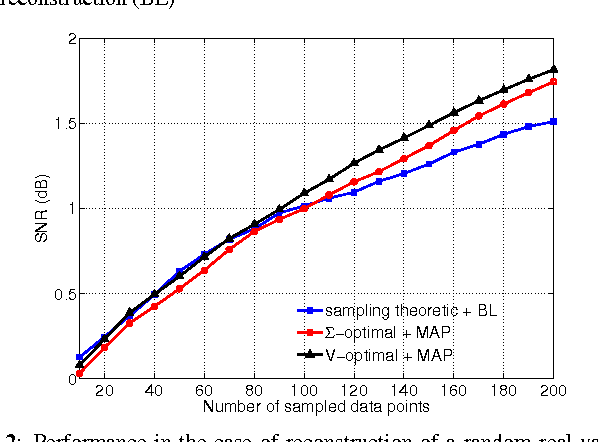
We give a probabilistic interpretation of sampling theory of graph signals. To do this, we first define a generative model for the data using a pairwise Gaussian random field (GRF) which depends on the graph. We show that, under certain conditions, reconstructing a graph signal from a subset of its samples by least squares is equivalent to performing MAP inference on an approximation of this GRF which has a low rank covariance matrix. We then show that a sampling set of given size with the largest associated cut-off frequency, which is optimal from a sampling theoretic point of view, minimizes the worst case predictive covariance of the MAP estimate on the GRF. This interpretation also gives an intuitive explanation for the superior performance of the sampling theoretic approach to active semi-supervised classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge