Active Semi-Supervised Learning Using Sampling Theory for Graph Signals
Paper and Code
May 16, 2014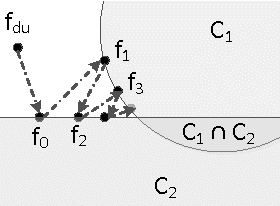
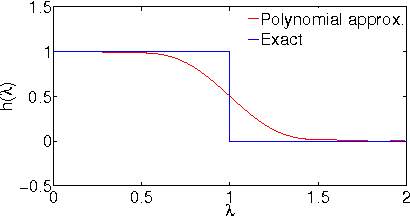
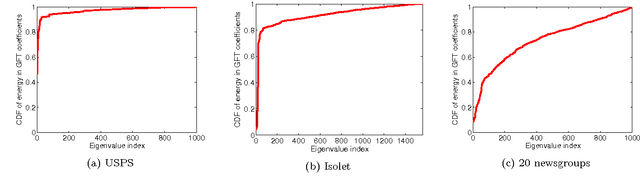
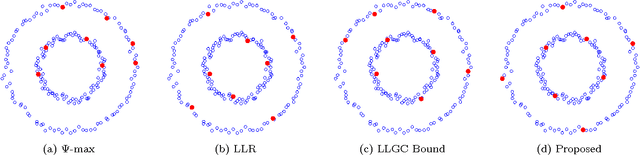
We consider the problem of offline, pool-based active semi-supervised learning on graphs. This problem is important when the labeled data is scarce and expensive whereas unlabeled data is easily available. The data points are represented by the vertices of an undirected graph with the similarity between them captured by the edge weights. Given a target number of nodes to label, the goal is to choose those nodes that are most informative and then predict the unknown labels. We propose a novel framework for this problem based on our recent results on sampling theory for graph signals. A graph signal is a real-valued function defined on each node of the graph. A notion of frequency for such signals can be defined using the spectrum of the graph Laplacian matrix. The sampling theory for graph signals aims to extend the traditional Nyquist-Shannon sampling theory by allowing us to identify the class of graph signals that can be reconstructed from their values on a subset of vertices. This approach allows us to define a criterion for active learning based on sampling set selection which aims at maximizing the frequency of the signals that can be reconstructed from their samples on the set. Experiments show the effectiveness of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge