A Sampling Theory Perspective of Graph-based Semi-supervised Learning

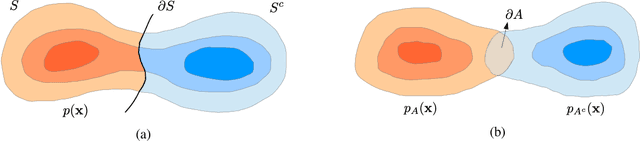
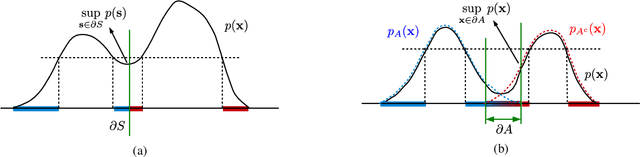
Graph-based methods have been quite successful in solving unsupervised and semi-supervised learning problems, as they provide a means to capture the underlying geometry of the dataset. It is often desirable for the constructed graph to satisfy two properties: first, data points that are similar in the feature space should be strongly connected on the graph, and second, the class label information should vary smoothly with respect to the graph, where smoothness is measured using the spectral properties of the graph Laplacian matrix. Recent works have justified some of these smoothness conditions by showing that they are strongly linked to the semi-supervised smoothness assumption and its variants. In this work, we reinforce this connection by viewing the problem from a graph sampling theoretic perspective, where class indicator functions are treated as bandlimited graph signals (in the eigenvector basis of the graph Laplacian) and label prediction as a bandlimited reconstruction problem. Our approach involves analyzing the bandwidth of class indicator signals generated from statistical data models with separable and nonseparable classes. These models are quite general and mimic the nature of most real-world datasets. Our results show that in the asymptotic limit, the bandwidth of any class indicator is also closely related to the geometry of the dataset. This allows one to theoretically justify the assumption of bandlimitedness of class indicator signals, thereby providing a sampling theoretic interpretation of graph-based semi-supervised classification.

Asymptotic Justification of Bandlimited Interpolation of Graph signals for Semi-Supervised Learning

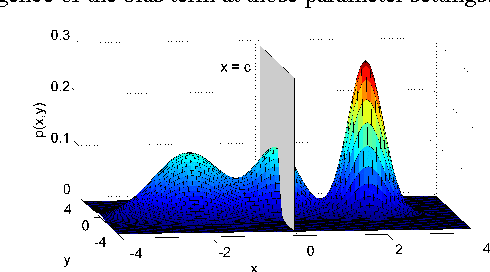
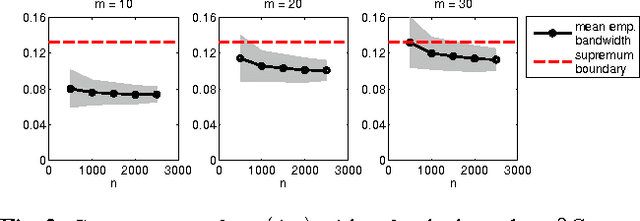
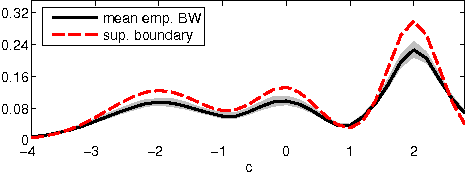
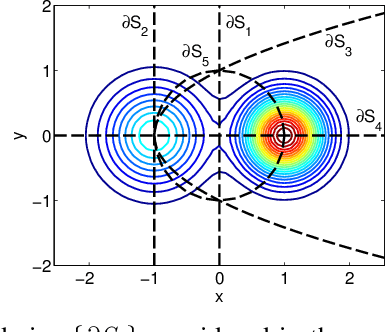
Graph-based methods play an important role in unsupervised and semi-supervised learning tasks by taking into account the underlying geometry of the data set. In this paper, we consider a statistical setting for semi-supervised learning and provide a formal justification of the recently introduced framework of bandlimited interpolation of graph signals. Our analysis leads to the interpretation that, given enough labeled data, this method is very closely related to a constrained low density separation problem as the number of data points tends to infinity. We demonstrate the practical utility of our results through simple experiments.

Active Semi-Supervised Learning Using Sampling Theory for Graph Signals

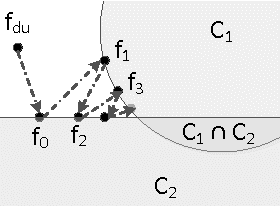
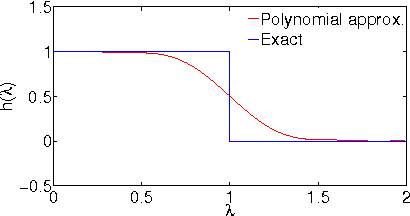
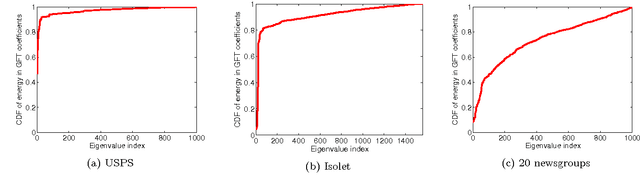
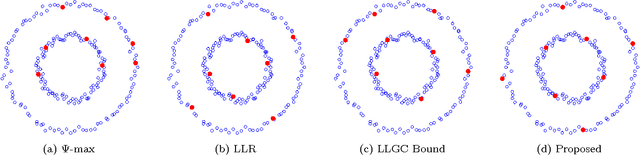
We consider the problem of offline, pool-based active semi-supervised learning on graphs. This problem is important when the labeled data is scarce and expensive whereas unlabeled data is easily available. The data points are represented by the vertices of an undirected graph with the similarity between them captured by the edge weights. Given a target number of nodes to label, the goal is to choose those nodes that are most informative and then predict the unknown labels. We propose a novel framework for this problem based on our recent results on sampling theory for graph signals. A graph signal is a real-valued function defined on each node of the graph. A notion of frequency for such signals can be defined using the spectrum of the graph Laplacian matrix. The sampling theory for graph signals aims to extend the traditional Nyquist-Shannon sampling theory by allowing us to identify the class of graph signals that can be reconstructed from their values on a subset of vertices. This approach allows us to define a criterion for active learning based on sampling set selection which aims at maximizing the frequency of the signals that can be reconstructed from their samples on the set. Experiments show the effectiveness of our method.