Approximation Algorithms for Combinatorial Optimization with Predictions

We initiate a systematic study of utilizing predictions to improve over approximation guarantees of classic algorithms, without increasing the running time. We propose a systematic method for a wide class of optimization problems that ask to select a feasible subset of input items of minimal (or maximal) total weight. This gives simple (near-)linear time algorithms for, e.g., Vertex Cover, Steiner Tree, Min-Weight Perfect Matching, Knapsack, and Clique. Our algorithms produce optimal solutions when provided with perfect predictions and their approximation ratios smoothly degrade with increasing prediction error. With small enough prediction error we achieve approximation guarantees that are beyond reach without predictions in the given time bounds, as exemplified by the NP-hardness and APX-hardness of many of the above problems. Although we show our approach to be optimal for this class of problems as a whole, there is a potential for exploiting specific structural properties of individual problems to obtain improved bounds; we demonstrate this on the Steiner Tree problem. We conclude with an empirical evaluation of our approach.

Connectivity Oracles for Predictable Vertex Failures

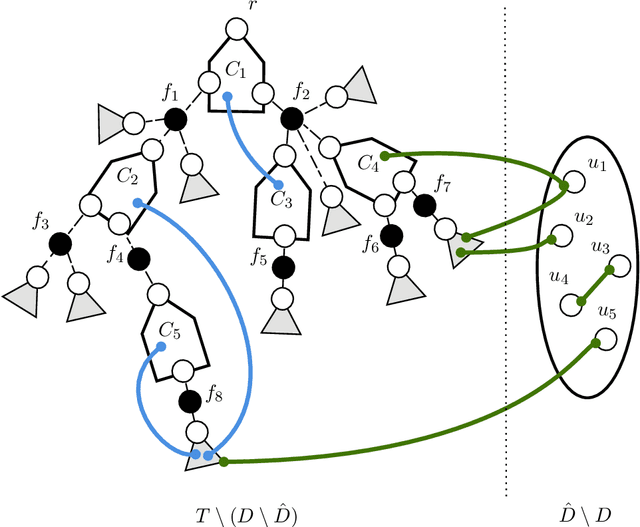
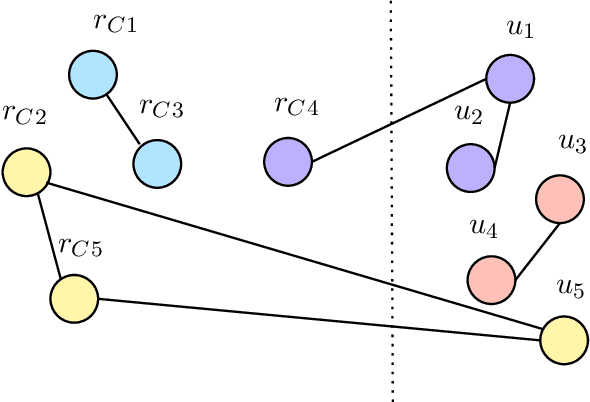
The problem of designing connectivity oracles supporting vertex failures is one of the basic data structures problems for undirected graphs. It is already well understood: previous works [Duan--Pettie STOC'10; Long--Saranurak FOCS'22] achieve query time linear in the number of failed vertices, and it is conditionally optimal as long as we require preprocessing time polynomial in the size of the graph and update time polynomial in the number of failed vertices. We revisit this problem in the paradigm of algorithms with predictions: we ask if the query time can be improved if the set of failed vertices can be predicted beforehand up to a small number of errors. More specifically, we design a data structure that, given a graph $G=(V,E)$ and a set of vertices predicted to fail $\widehat{D} \subseteq V$ of size $d=|\widehat{D}|$, preprocesses it in time $\tilde{O}(d|E|)$ and then can receive an update given as the symmetric difference between the predicted and the actual set of failed vertices $\widehat{D} \triangle D = (\widehat{D} \setminus D) \cup (D \setminus \widehat{D})$ of size $\eta = |\widehat{D} \triangle D|$, process it in time $\tilde{O}(\eta^4)$, and after that answer connectivity queries in $G \setminus D$ in time $O(\eta)$. Viewed from another perspective, our data structure provides an improvement over the state of the art for the \emph{fully dynamic subgraph connectivity problem} in the \emph{sensitivity setting} [Henzinger--Neumann ESA'16]. We argue that the preprocessing time and query time of our data structure are conditionally optimal under standard fine-grained complexity assumptions.

Mixing predictions for online metric algorithms

A major technique in learning-augmented online algorithms is combining multiple algorithms or predictors. Since the performance of each predictor may vary over time, it is desirable to use not the single best predictor as a benchmark, but rather a dynamic combination which follows different predictors at different times. We design algorithms that combine predictions and are competitive against such dynamic combinations for a wide class of online problems, namely, metrical task systems. Against the best (in hindsight) unconstrained combination of $\ell$ predictors, we obtain a competitive ratio of $O(\ell^2)$, and show that this is best possible. However, for a benchmark with slightly constrained number of switches between different predictors, we can get a $(1+\epsilon)$-competitive algorithm. Moreover, our algorithms can be adapted to access predictors in a bandit-like fashion, querying only one predictor at a time. An unexpected implication of one of our lower bounds is a new structural insight about covering formulations for the $k$-server problem.

Paging with Succinct Predictions

Paging is a prototypical problem in the area of online algorithms. It has also played a central role in the development of learning-augmented algorithms -- a recent line of research that aims to ameliorate the shortcomings of classical worst-case analysis by giving algorithms access to predictions. Such predictions can typically be generated using a machine learning approach, but they are inherently imperfect. Previous work on learning-augmented paging has investigated predictions on (i) when the current page will be requested again (reoccurrence predictions), (ii) the current state of the cache in an optimal algorithm (state predictions), (iii) all requests until the current page gets requested again, and (iv) the relative order in which pages are requested. We study learning-augmented paging from the new perspective of requiring the least possible amount of predicted information. More specifically, the predictions obtained alongside each page request are limited to one bit only. We consider two natural such setups: (i) discard predictions, in which the predicted bit denotes whether or not it is ``safe'' to evict this page, and (ii) phase predictions, where the bit denotes whether the current page will be requested in the next phase (for an appropriate partitioning of the input into phases). We develop algorithms for each of the two setups that satisfy all three desirable properties of learning-augmented algorithms -- that is, they are consistent, robust and smooth -- despite being limited to a one-bit prediction per request. We also present lower bounds establishing that our algorithms are essentially best possible.

Learning-Augmented Maximum Flow

We propose a framework for speeding up maximum flow computation by using predictions. A prediction is a flow, i.e., an assignment of non-negative flow values to edges, which satisfies the flow conservation property, but does not necessarily respect the edge capacities of the actual instance (since these were unknown at the time of learning). We present an algorithm that, given an $m$-edge flow network and a predicted flow, computes a maximum flow in $O(m\eta)$ time, where $\eta$ is the $\ell_1$ error of the prediction, i.e., the sum over the edges of the absolute difference between the predicted and optimal flow values. Moreover, we prove that, given an oracle access to a distribution over flow networks, it is possible to efficiently PAC-learn a prediction minimizing the expected $\ell_1$ error over that distribution. Our results fit into the recent line of research on learning-augmented algorithms, which aims to improve over worst-case bounds of classical algorithms by using predictions, e.g., machine-learned from previous similar instances. So far, the main focus in this area was on improving competitive ratios for online problems. Following Dinitz et al. (NeurIPS 2021), our results are one of the firsts to improve the running time of an offline problem.

Learning-Augmented Dynamic Power Management with Multiple States via New Ski Rental Bounds

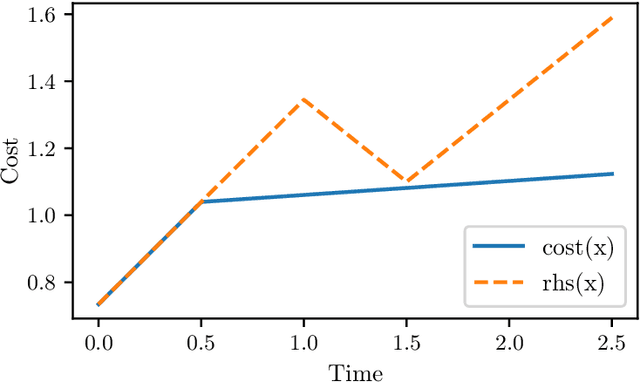
We study the online problem of minimizing power consumption in systems with multiple power-saving states. During idle periods of unknown lengths, an algorithm has to choose between power-saving states of different energy consumption and wake-up costs. We develop a learning-augmented online algorithm that makes decisions based on (potentially inaccurate) predicted lengths of the idle periods. The algorithm's performance is near-optimal when predictions are accurate and degrades gracefully with increasing prediction error, with a worst-case guarantee almost identical to the optimal classical online algorithm for the problem. A key ingredient in our approach is a new algorithm for the online ski rental problem in the learning augmented setting with tight dependence on the prediction error. We support our theoretical findings with experiments.

Nearly-Tight and Oblivious Algorithms for Explainable Clustering

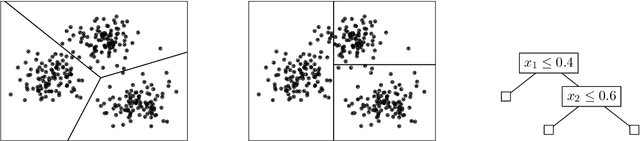
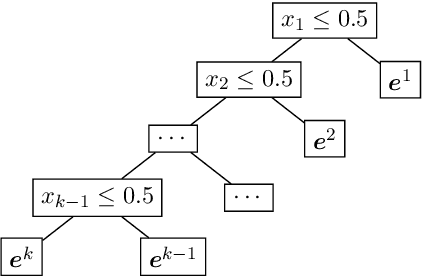
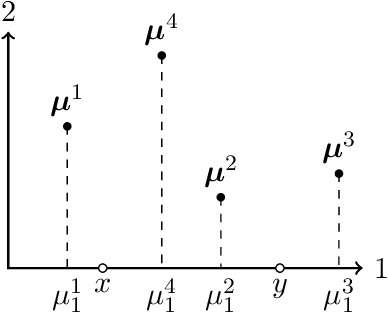
We study the problem of explainable clustering in the setting first formalized by Moshkovitz, Dasgupta, Rashtchian, and Frost (ICML 2020). A $k$-clustering is said to be explainable if it is given by a decision tree where each internal node splits data points with a threshold cut in a single dimension (feature), and each of the $k$ leaves corresponds to a cluster. We give an algorithm that outputs an explainable clustering that loses at most a factor of $O(\log^2 k)$ compared to an optimal (not necessarily explainable) clustering for the $k$-medians objective, and a factor of $O(k \log^2 k)$ for the $k$-means objective. This improves over the previous best upper bounds of $O(k)$ and $O(k^2)$, respectively, and nearly matches the previous $\Omega(\log k)$ lower bound for $k$-medians and our new $\Omega(k)$ lower bound for $k$-means. The algorithm is remarkably simple. In particular, given an initial not necessarily explainable clustering in $\mathbb{R}^d$, it is oblivious to the data points and runs in time $O(dk \log^2 k)$, independent of the number of data points $n$. Our upper and lower bounds also generalize to objectives given by higher $\ell_p$-norms.

Robust Learning-Augmented Caching: An Experimental Study

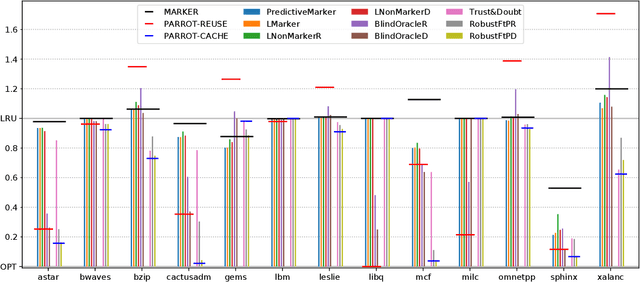
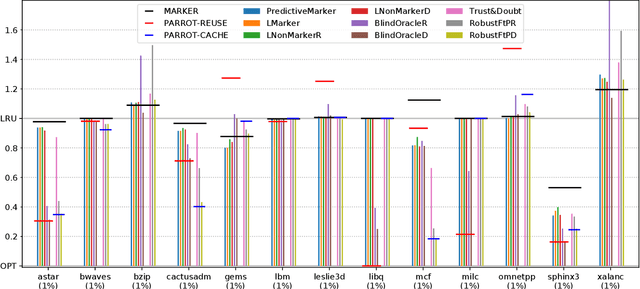
Effective caching is crucial for the performance of modern-day computing systems. A key optimization problem arising in caching -- which item to evict to make room for a new item -- cannot be optimally solved without knowing the future. There are many classical approximation algorithms for this problem, but more recently researchers started to successfully apply machine learning to decide what to evict by discovering implicit input patterns and predicting the future. While machine learning typically does not provide any worst-case guarantees, the new field of learning-augmented algorithms proposes solutions that leverage classical online caching algorithms to make the machine-learned predictors robust. We are the first to comprehensively evaluate these learning-augmented algorithms on real-world caching datasets and state-of-the-art machine-learned predictors. We show that a straightforward method -- blindly following either a predictor or a classical robust algorithm, and switching whenever one becomes worse than the other -- has only a low overhead over a well-performing predictor, while competing with classical methods when the coupled predictor fails, thus providing a cheap worst-case insurance.

Emotion Recognition Using Wearables: A Systematic Literature Review Work in progress

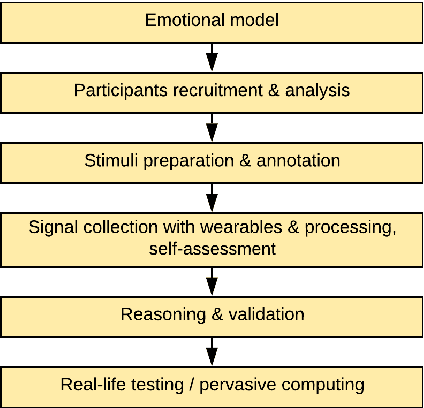
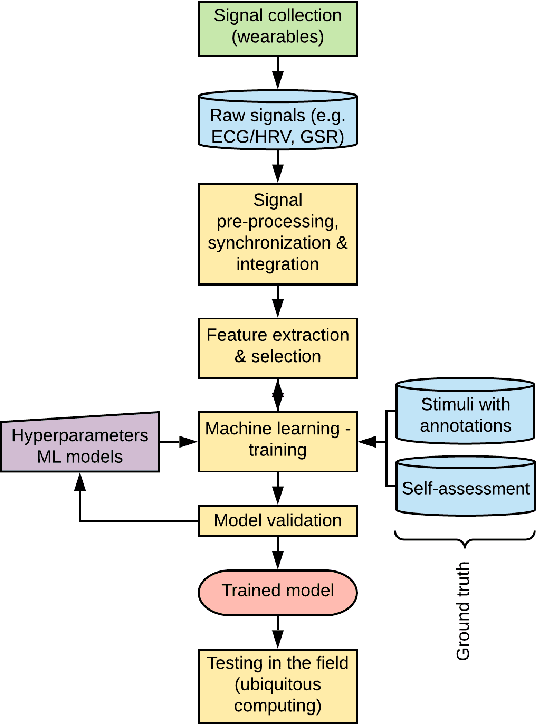
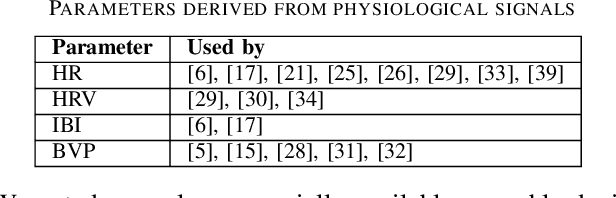
Wearables like smartwatches or wrist bands equipped with pervasive sensors enable us to monitor our physiological signals. In this study, we address the question whether they can help us to recognize our emotions in our everyday life for ubiquitous computing. Using the systematic literature review, we identified crucial research steps and discussed the main limitations and problems in the domain.

Flying, Hopping Pit-Bots for Cave and Lava Tube Exploration on the Moon and Mars

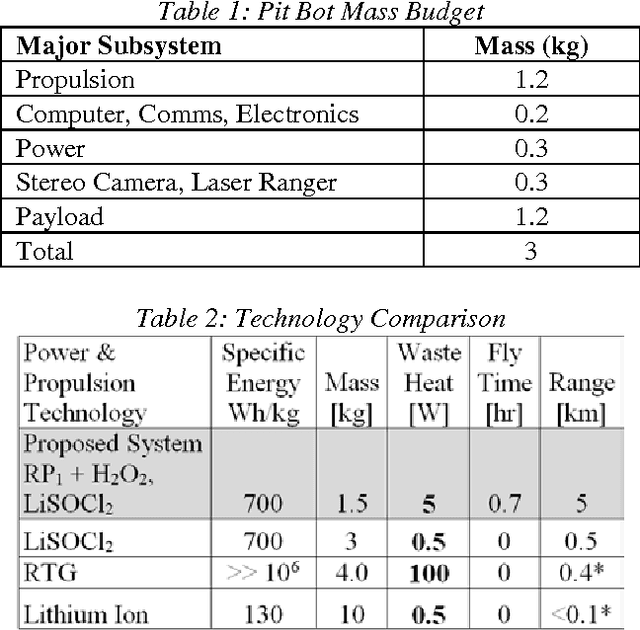
Wheeled ground robots are limited from exploring extreme environments such as caves, lava tubes and skylights. Small robots that utilize unconventional mobility through hopping, flying and rolling can overcome many roughness limitations and thus extend exploration sites of interest on Moon and Mars. In this paper we introduce a network of 3 kg, 0.30 m diameter ball robots (pit-bots) that can fly, hop and roll using an onboard miniature propulsion system. These pit-bots can be deployed from a lander or large rover. Each robot is equipped with a smartphone sized computer, stereo camera and laser rangefinder to per-form navigation and mapping. The ball robot can carry a payload of 1 kg or perform sample return. Our studies show a range of 5 km and 0.7 hours flight time on the Moon.