Learnable Infinite Taylor Gaussian for Dynamic View Rendering

Capturing the temporal evolution of Gaussian properties such as position, rotation, and scale is a challenging task due to the vast number of time-varying parameters and the limited photometric data available, which generally results in convergence issues, making it difficult to find an optimal solution. While feeding all inputs into an end-to-end neural network can effectively model complex temporal dynamics, this approach lacks explicit supervision and struggles to generate high-quality transformation fields. On the other hand, using time-conditioned polynomial functions to model Gaussian trajectories and orientations provides a more explicit and interpretable solution, but requires significant handcrafted effort and lacks generalizability across diverse scenes. To overcome these limitations, this paper introduces a novel approach based on a learnable infinite Taylor Formula to model the temporal evolution of Gaussians. This method offers both the flexibility of an implicit network-based approach and the interpretability of explicit polynomial functions, allowing for more robust and generalizable modeling of Gaussian dynamics across various dynamic scenes. Extensive experiments on dynamic novel view rendering tasks are conducted on public datasets, demonstrating that the proposed method achieves state-of-the-art performance in this domain. More information is available on our project page(https://ellisonking.github.io/TaylorGaussian).

Connectivity Oracles for Predictable Vertex Failures

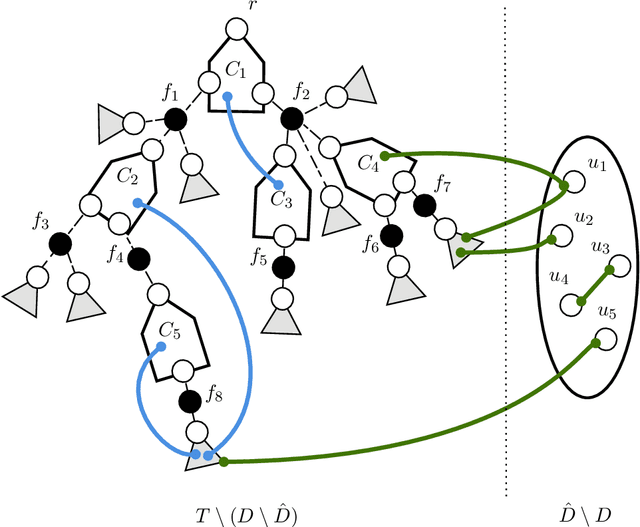
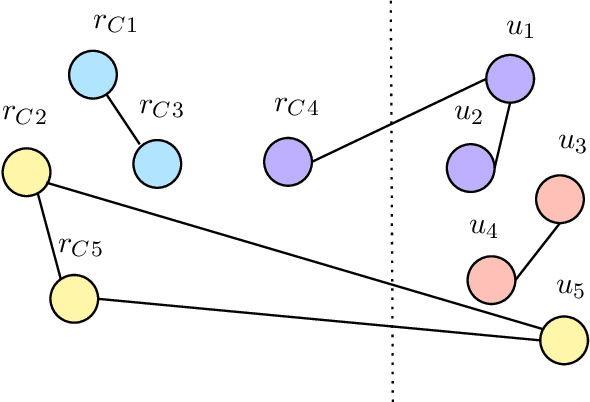
The problem of designing connectivity oracles supporting vertex failures is one of the basic data structures problems for undirected graphs. It is already well understood: previous works [Duan--Pettie STOC'10; Long--Saranurak FOCS'22] achieve query time linear in the number of failed vertices, and it is conditionally optimal as long as we require preprocessing time polynomial in the size of the graph and update time polynomial in the number of failed vertices. We revisit this problem in the paradigm of algorithms with predictions: we ask if the query time can be improved if the set of failed vertices can be predicted beforehand up to a small number of errors. More specifically, we design a data structure that, given a graph $G=(V,E)$ and a set of vertices predicted to fail $\widehat{D} \subseteq V$ of size $d=|\widehat{D}|$, preprocesses it in time $\tilde{O}(d|E|)$ and then can receive an update given as the symmetric difference between the predicted and the actual set of failed vertices $\widehat{D} \triangle D = (\widehat{D} \setminus D) \cup (D \setminus \widehat{D})$ of size $\eta = |\widehat{D} \triangle D|$, process it in time $\tilde{O}(\eta^4)$, and after that answer connectivity queries in $G \setminus D$ in time $O(\eta)$. Viewed from another perspective, our data structure provides an improvement over the state of the art for the \emph{fully dynamic subgraph connectivity problem} in the \emph{sensitivity setting} [Henzinger--Neumann ESA'16]. We argue that the preprocessing time and query time of our data structure are conditionally optimal under standard fine-grained complexity assumptions.

HAHE: Hierarchical Attentive Heterogeneous Information Network Embedding

Given the intractability of large scale HIN, network embedding which learns low dimensional proximity-preserved representations for nodes in the new space becomes a natural way to analyse HIN. However, two challenges arise in HIN embedding. (1) Different HIN structures with different semantic meanings play different roles in capturing relationships among nodes in HIN, how can we learn personalized preferences over different meta-paths for each individual node in HIN? (2) With the number of large scale HIN increasing dramatically in various web services, how can we update the embedding information of new nodes in an efficient way? To tackle these challenges, we propose a Hierarchical Attentive Heterogeneous information network Embedding (HAHE ) model which is capable of learning personalized meta-path preferences for each node as well as updating the embedding information for each new node efficiently with only its neighbor node information. The proposed HAHE model extracts the semantic relationships among nodes in the semantic space based on different meta-paths and adopts a neighborhood attention layer to conduct weighted aggregations of neighborhood structure features for each node, enabling the embedding information of each new node to be updated efficiently. Besides, a meta-path attention layer is also employed to learn the personalized meta-path preferences for each individual node. Extensive experiments on several real-world datasets show that our proposed HAHE model significantly outperforms the state-of-the-art methods in terms of various evaluation metrics.