Recent Advances on Generalizable Diffusion-generated Image Detection

The rise of diffusion models has significantly improved the fidelity and diversity of generated images. With numerous benefits, these advancements also introduce new risks. Diffusion models can be exploited to create high-quality Deepfake images, which poses challenges for image authenticity verification. In recent years, research on generalizable diffusion-generated image detection has grown rapidly. However, a comprehensive review of this topic is still lacking. To bridge this gap, we present a systematic survey of recent advances and classify them into two main categories: (1) data-driven detection and (2) feature-driven detection. Existing detection methods are further classified into six fine-grained categories based on their underlying principles. Finally, we identify several open challenges and envision some future directions, with the hope of inspiring more research work on this important topic. Reviewed works in this survey can be found at https://github.com/zju-pi/Awesome-Diffusion-generated-Image-Detection.

DICE: Distilling Classifier-Free Guidance into Text Embeddings

Text-to-image diffusion models are capable of generating high-quality images, but these images often fail to align closely with the given text prompts. Classifier-free guidance (CFG) is a popular and effective technique for improving text-image alignment in the generative process. However, using CFG introduces significant computational overhead and deviates from the established theoretical foundations of diffusion models. In this paper, we present DIstilling CFG by enhancing text Embeddings (DICE), a novel approach that removes the reliance on CFG in the generative process while maintaining the benefits it provides. DICE distills a CFG-based text-to-image diffusion model into a CFG-free version by refining text embeddings to replicate CFG-based directions. In this way, we avoid the computational and theoretical drawbacks of CFG, enabling high-quality, well-aligned image generation at a fast sampling speed. Extensive experiments on multiple Stable Diffusion v1.5 variants, SDXL and PixArt-$\alpha$ demonstrate the effectiveness of our method. Furthermore, DICE supports negative prompts for image editing to improve image quality further. Code will be available soon.

Simple and Fast Distillation of Diffusion Models

Diffusion-based generative models have demonstrated their powerful performance across various tasks, but this comes at a cost of the slow sampling speed. To achieve both efficient and high-quality synthesis, various distillation-based accelerated sampling methods have been developed recently. However, they generally require time-consuming fine tuning with elaborate designs to achieve satisfactory performance in a specific number of function evaluation (NFE), making them difficult to employ in practice. To address this issue, we propose Simple and Fast Distillation (SFD) of diffusion models, which simplifies the paradigm used in existing methods and largely shortens their fine-tuning time up to 1000$\times$. We begin with a vanilla distillation-based sampling method and boost its performance to state of the art by identifying and addressing several small yet vital factors affecting the synthesis efficiency and quality. Our method can also achieve sampling with variable NFEs using a single distilled model. Extensive experiments demonstrate that SFD strikes a good balance between the sample quality and fine-tuning costs in few-step image generation task. For example, SFD achieves 4.53 FID (NFE=2) on CIFAR-10 with only 0.64 hours of fine-tuning on a single NVIDIA A100 GPU. Our code is available at https://github.com/zju-pi/diff-sampler.

Conditional Image Synthesis with Diffusion Models: A Survey

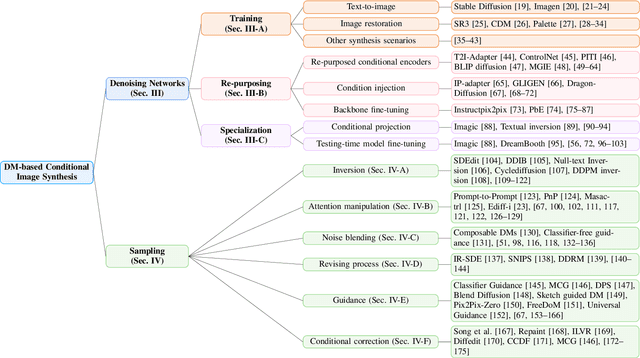
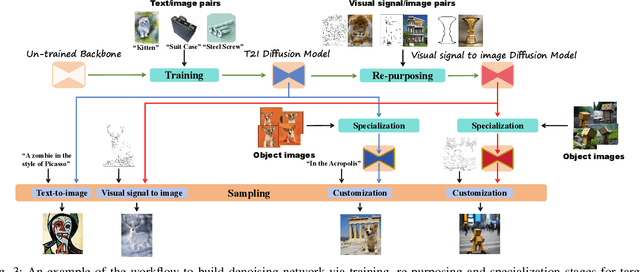
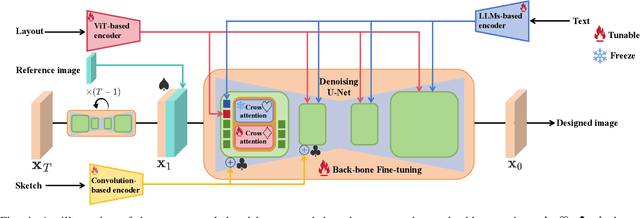
Conditional image synthesis based on user-specified requirements is a key component in creating complex visual content. In recent years, diffusion-based generative modeling has become a highly effective way for conditional image synthesis, leading to exponential growth in the literature. However, the complexity of diffusion-based modeling, the wide range of image synthesis tasks, and the diversity of conditioning mechanisms present significant challenges for researchers to keep up with rapid developments and understand the core concepts on this topic. In this survey, we categorize existing works based on how conditions are integrated into the two fundamental components of diffusion-based modeling, i.e., the denoising network and the sampling process. We specifically highlight the underlying principles, advantages, and potential challenges of various conditioning approaches in the training, re-purposing, and specialization stages to construct a desired denoising network. We also summarize six mainstream conditioning mechanisms in the essential sampling process. All discussions are centered around popular applications. Finally, we pinpoint some critical yet still open problems to be solved in the future and suggest some possible solutions. Our reviewed works are itemized at https://github.com/zju-pi/Awesome-Conditional-Diffusion-Models.

Knowledge Distillation with Refined Logits

Recent research on knowledge distillation has increasingly focused on logit distillation because of its simplicity, effectiveness, and versatility in model compression. In this paper, we introduce Refined Logit Distillation (RLD) to address the limitations of current logit distillation methods. Our approach is motivated by the observation that even high-performing teacher models can make incorrect predictions, creating a conflict between the standard distillation loss and the cross-entropy loss. This conflict can undermine the consistency of the student model's learning objectives. Previous attempts to use labels to empirically correct teacher predictions may undermine the class correlation. In contrast, our RLD employs labeling information to dynamically refine teacher logits. In this way, our method can effectively eliminate misleading information from the teacher while preserving crucial class correlations, thus enhancing the value and efficiency of distilled knowledge. Experimental results on CIFAR-100 and ImageNet demonstrate its superiority over existing methods. The code is provided at \text{https://github.com/zju-SWJ/RLD}.

On the Trajectory Regularity of ODE-based Diffusion Sampling

Diffusion-based generative models use stochastic differential equations (SDEs) and their equivalent ordinary differential equations (ODEs) to establish a smooth connection between a complex data distribution and a tractable prior distribution. In this paper, we identify several intriguing trajectory properties in the ODE-based sampling process of diffusion models. We characterize an implicit denoising trajectory and discuss its vital role in forming the coupled sampling trajectory with a strong shape regularity, regardless of the generated content. We also describe a dynamic programming-based scheme to make the time schedule in sampling better fit the underlying trajectory structure. This simple strategy requires minimal modification to any given ODE-based numerical solvers and incurs negligible computational cost, while delivering superior performance in image generation, especially in $5\sim 10$ function evaluations.

Knowledge Translation: A New Pathway for Model Compression

Deep learning has witnessed significant advancements in recent years at the cost of increasing training, inference, and model storage overhead. While existing model compression methods strive to reduce the number of model parameters while maintaining high accuracy, they inevitably necessitate the re-training of the compressed model or impose architectural constraints. To overcome these limitations, this paper presents a novel framework, termed \textbf{K}nowledge \textbf{T}ranslation (KT), wherein a ``translation'' model is trained to receive the parameters of a larger model and generate compressed parameters. The concept of KT draws inspiration from language translation, which effectively employs neural networks to convert different languages, maintaining identical meaning. Accordingly, we explore the potential of neural networks to convert models of disparate sizes, while preserving their functionality. We propose a comprehensive framework for KT, introduce data augmentation strategies to enhance model performance despite restricted training data, and successfully demonstrate the feasibility of KT on the MNIST dataset. Code is available at \url{https://github.com/zju-SWJ/KT}.

Fast ODE-based Sampling for Diffusion Models in Around 5 Steps

Sampling from diffusion models can be treated as solving the corresponding ordinary differential equations (ODEs), with the aim of obtaining an accurate solution with as few number of function evaluations (NFE) as possible. Recently, various fast samplers utilizing higher-order ODE solvers have emerged and achieved better performance than the initial first-order one. However, these numerical methods inherently result in certain approximation errors, which significantly degrades sample quality with extremely small NFE (e.g., around 5). In contrast, based on the geometric observation that each sampling trajectory almost lies in a two-dimensional subspace embedded in the ambient space, we propose Approximate MEan-Direction Solver (AMED-Solver) that eliminates truncation errors by directly learning the mean direction for fast diffusion sampling. Besides, our method can be easily used as a plugin to further improve existing ODE-based samplers. Extensive experiments on image synthesis with the resolution ranging from 32 to 256 demonstrate the effectiveness of our method. With only 5 NFE, we achieve 7.14 FID on CIFAR-10, 13.75 FID on ImageNet 64$\times$64, and 12.79 FID on LSUN Bedroom. Our code is available at https://github.com/zhyzhouu/amed-solver.

Customizing Synthetic Data for Data-Free Student Learning

Data-free knowledge distillation (DFKD) aims to obtain a lightweight student model without original training data. Existing works generally synthesize data from the pre-trained teacher model to replace the original training data for student learning. To more effectively train the student model, the synthetic data shall be customized to the current student learning ability. However, this is ignored in the existing DFKD methods and thus negatively affects the student training. To address this issue, we propose Customizing Synthetic Data for Data-Free Student Learning (CSD) in this paper, which achieves adaptive data synthesis using a self-supervised augmented auxiliary task to estimate the student learning ability. Specifically, data synthesis is dynamically adjusted to enlarge the cross entropy between the labels and the predictions from the self-supervised augmented task, thus generating hard samples for the student model. The experiments on various datasets and teacher-student models show the effectiveness of our proposed method. Code is available at: $\href{https://github.com/luoshiya/CSD}{https://github.com/luoshiya/CSD}$

Adaptive Multi-Teacher Knowledge Distillation with Meta-Learning

Multi-Teacher knowledge distillation provides students with additional supervision from multiple pre-trained teachers with diverse information sources. Most existing methods explore different weighting strategies to obtain a powerful ensemble teacher, while ignoring the student with poor learning ability may not benefit from such specialized integrated knowledge. To address this problem, we propose Adaptive Multi-teacher Knowledge Distillation with Meta-Learning (MMKD) to supervise student with appropriate knowledge from a tailored ensemble teacher. With the help of a meta-weight network, the diverse yet compatible teacher knowledge in the output layer and intermediate layers is jointly leveraged to enhance the student performance. Extensive experiments on multiple benchmark datasets validate the effectiveness and flexibility of our methods. Code is available: https://github.com/Rorozhl/MMKD.