Evangelos Kosinas
Connectivity Oracles for Predictable Vertex Failures
Dec 13, 2023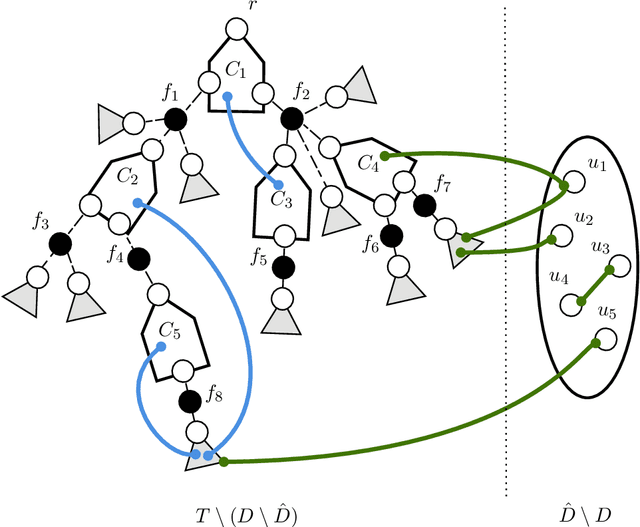
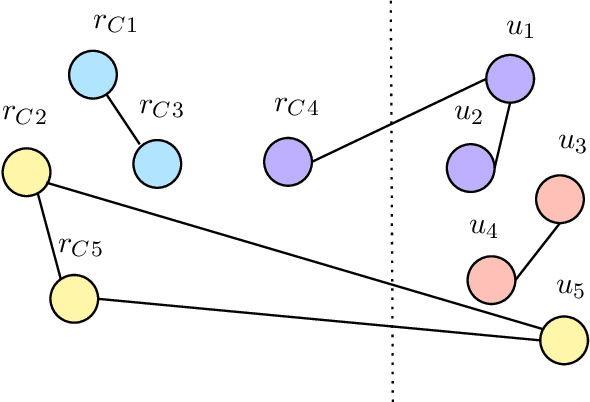
Abstract:The problem of designing connectivity oracles supporting vertex failures is one of the basic data structures problems for undirected graphs. It is already well understood: previous works [Duan--Pettie STOC'10; Long--Saranurak FOCS'22] achieve query time linear in the number of failed vertices, and it is conditionally optimal as long as we require preprocessing time polynomial in the size of the graph and update time polynomial in the number of failed vertices. We revisit this problem in the paradigm of algorithms with predictions: we ask if the query time can be improved if the set of failed vertices can be predicted beforehand up to a small number of errors. More specifically, we design a data structure that, given a graph $G=(V,E)$ and a set of vertices predicted to fail $\widehat{D} \subseteq V$ of size $d=|\widehat{D}|$, preprocesses it in time $\tilde{O}(d|E|)$ and then can receive an update given as the symmetric difference between the predicted and the actual set of failed vertices $\widehat{D} \triangle D = (\widehat{D} \setminus D) \cup (D \setminus \widehat{D})$ of size $\eta = |\widehat{D} \triangle D|$, process it in time $\tilde{O}(\eta^4)$, and after that answer connectivity queries in $G \setminus D$ in time $O(\eta)$. Viewed from another perspective, our data structure provides an improvement over the state of the art for the \emph{fully dynamic subgraph connectivity problem} in the \emph{sensitivity setting} [Henzinger--Neumann ESA'16]. We argue that the preprocessing time and query time of our data structure are conditionally optimal under standard fine-grained complexity assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge