Learning-Augmented Priority Queues

Priority queues are one of the most fundamental and widely used data structures in computer science. Their primary objective is to efficiently support the insertion of new elements with assigned priorities and the extraction of the highest priority element. In this study, we investigate the design of priority queues within the learning-augmented framework, where algorithms use potentially inaccurate predictions to enhance their worst-case performance. We examine three prediction models spanning different use cases, and show how the predictions can be leveraged to enhance the performance of priority queue operations. Moreover, we demonstrate the optimality of our solution and discuss some possible applications.

Sorting with Predictions

We explore the fundamental problem of sorting through the lens of learning-augmented algorithms, where algorithms can leverage possibly erroneous predictions to improve their efficiency. We consider two different settings: In the first setting, each item is provided a prediction of its position in the sorted list. In the second setting, we assume there is a "quick-and-dirty" way of comparing items, in addition to slow-and-exact comparisons. For both settings, we design new and simple algorithms using only $O(\sum_i \log \eta_i)$ exact comparisons, where $\eta_i$ is a suitably defined prediction error for the $i$th element. In particular, as the quality of predictions deteriorates, the number of comparisons degrades smoothly from $O(n)$ to $O(n\log n)$. We prove that the comparison complexity is theoretically optimal with respect to the examined error measures. An experimental evaluation against existing adaptive and non-adaptive sorting algorithms demonstrates the potential of applying learning-augmented algorithms in sorting tasks.

Mixing predictions for online metric algorithms

A major technique in learning-augmented online algorithms is combining multiple algorithms or predictors. Since the performance of each predictor may vary over time, it is desirable to use not the single best predictor as a benchmark, but rather a dynamic combination which follows different predictors at different times. We design algorithms that combine predictions and are competitive against such dynamic combinations for a wide class of online problems, namely, metrical task systems. Against the best (in hindsight) unconstrained combination of $\ell$ predictors, we obtain a competitive ratio of $O(\ell^2)$, and show that this is best possible. However, for a benchmark with slightly constrained number of switches between different predictors, we can get a $(1+\epsilon)$-competitive algorithm. Moreover, our algorithms can be adapted to access predictors in a bandit-like fashion, querying only one predictor at a time. An unexpected implication of one of our lower bounds is a new structural insight about covering formulations for the $k$-server problem.

Learning-Augmented Dynamic Power Management with Multiple States via New Ski Rental Bounds

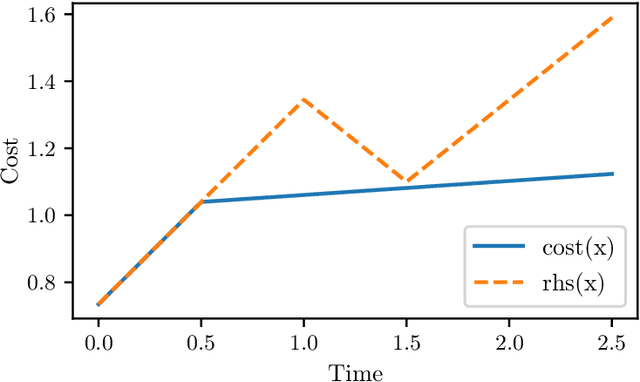
We study the online problem of minimizing power consumption in systems with multiple power-saving states. During idle periods of unknown lengths, an algorithm has to choose between power-saving states of different energy consumption and wake-up costs. We develop a learning-augmented online algorithm that makes decisions based on (potentially inaccurate) predicted lengths of the idle periods. The algorithm's performance is near-optimal when predictions are accurate and degrades gracefully with increasing prediction error, with a worst-case guarantee almost identical to the optimal classical online algorithm for the problem. A key ingredient in our approach is a new algorithm for the online ski rental problem in the learning augmented setting with tight dependence on the prediction error. We support our theoretical findings with experiments.