Latent fingerprint enhancement for accurate minutiae detection

Identification of suspects based on partial and smudged fingerprints, commonly referred to as fingermarks or latent fingerprints, presents a significant challenge in the field of fingerprint recognition. Although fixed-length embeddings have shown effectiveness in recognising rolled and slap fingerprints, the methods for matching latent fingerprints have primarily centred around local minutiae-based embeddings, failing to fully exploit global representations for matching purposes. Consequently, enhancing latent fingerprints becomes critical to ensuring robust identification for forensic investigations. Current approaches often prioritise restoring ridge patterns, overlooking the fine-macroeconomic details crucial for accurate fingerprint recognition. To address this, we propose a novel approach that uses generative adversary networks (GANs) to redefine Latent Fingerprint Enhancement (LFE) through a structured approach to fingerprint generation. By directly optimising the minutiae information during the generation process, the model produces enhanced latent fingerprints that exhibit exceptional fidelity to ground-truth instances. This leads to a significant improvement in identification performance. Our framework integrates minutiae locations and orientation fields, ensuring the preservation of both local and structural fingerprint features. Extensive evaluations conducted on two publicly available datasets demonstrate our method's dominance over existing state-of-the-art techniques, highlighting its potential to significantly enhance latent fingerprint recognition accuracy in forensic applications.

Multipolar Acoustic Source Reconstruction from Sparse Far-Field Data using ALOHA

The reconstruction of multipolar acoustic or electromagnetic sources from their far-field radiation patterns plays a crucial role in numerous practical applications. Most of the existing techniques for source reconstruction require dense multi-frequency data at the Nyquist sampling rate. Accessibility of only sparse data at a sub-sampled grid contributes to the null space of the inverse source-to-data operator, which causes significant imaging artifacts. For this purpose, additional knowledge about the source or regularization is required. In this article, we propose a novel two-stage strategy for multipolar source reconstruction from the sub-sampled sparse data that takes advantage of the sparsity of the sources in the physical domain. The data at the Nyquist sampling rate is recovered from sub-sampled data and then a conventional inversion algorithm is used to reconstruct sources. The data recovery problem is linked to a spectrum recovery problem for the signal with the finite rate of innovations (FIR) that is solved using an annihilating filter-based structured Hankel matrix completion approach (ALOHA). For an accurate reconstruction of multipolar sources, we employ a Fourier inversion algorithm. The suitability of the suggested approach for both noisy and noise-free measurements is supported by numerical evidence.

Anticancer Peptides Classification using Kernel Sparse Representation Classifier

Cancer is one of the most challenging diseases because of its complexity, variability, and diversity of causes. It has been one of the major research topics over the past decades, yet it is still poorly understood. To this end, multifaceted therapeutic frameworks are indispensable. \emph{Anticancer peptides} (ACPs) are the most promising treatment option, but their large-scale identification and synthesis require reliable prediction methods, which is still a problem. In this paper, we present an intuitive classification strategy that differs from the traditional \emph{black box} method and is based on the well-known statistical theory of \emph{sparse-representation classification} (SRC). Specifically, we create over-complete dictionary matrices by embedding the \emph{composition of the K-spaced amino acid pairs} (CKSAAP). Unlike the traditional SRC frameworks, we use an efficient \emph{matching pursuit} solver instead of the computationally expensive \emph{basis pursuit} solver in this strategy. Furthermore, the \emph{kernel principal component analysis} (KPCA) is employed to cope with non-linearity and dimension reduction of the feature space whereas the \emph{synthetic minority oversampling technique} (SMOTE) is used to balance the dictionary. The proposed method is evaluated on two benchmark datasets for well-known statistical parameters and is found to outperform the existing methods. The results show the highest sensitivity with the most balanced accuracy, which might be beneficial in understanding structural and chemical aspects and developing new ACPs. The Google-Colab implementation of the proposed method is available at the author's GitHub page (\href{https://github.com/ehtisham-Fazal/ACP-Kernel-SRC}{https://github.com/ehtisham-fazal/ACP-Kernel-SRC}).

Performance Analysis of Fractional Learning Algorithms

Fractional learning algorithms are trending in signal processing and adaptive filtering recently. However, it is unclear whether the proclaimed superiority over conventional algorithms is well-grounded or is a myth as their performance has never been extensively analyzed. In this article, a rigorous analysis of fractional variants of the least mean squares and steepest descent algorithms is performed. Some critical schematic kinks in fractional learning algorithms are identified. Their origins and consequences on the performance of the learning algorithms are discussed and swift ready-witted remedies are proposed. Apposite numerical experiments are conducted to discuss the convergence and efficiency of the fractional learning algorithms in stochastic environments.

Short-Term Load Forecasting using Bi-directional Sequential Models and Feature Engineering for Small Datasets

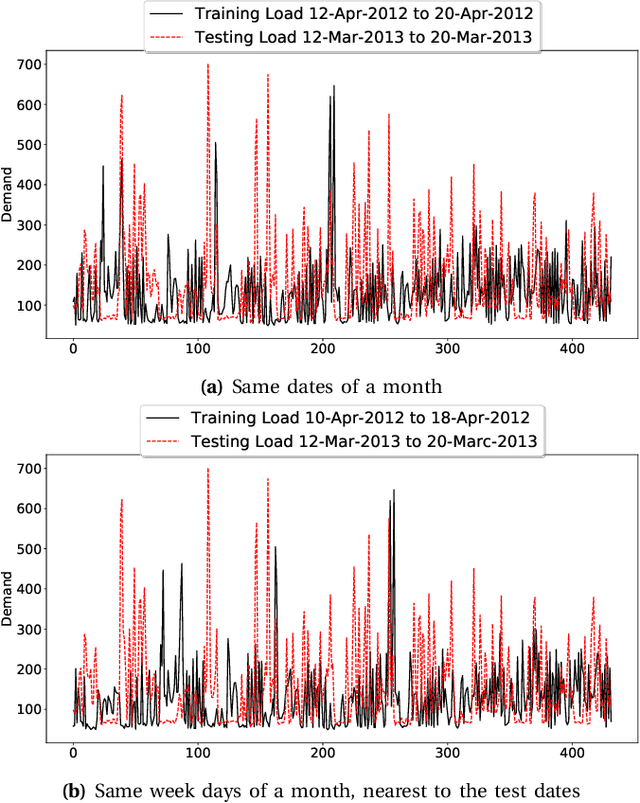
Electricity load forecasting enables the grid operators to optimally implement the smart grid's most essential features such as demand response and energy efficiency. Electricity demand profiles can vary drastically from one region to another on diurnal, seasonal and yearly scale. Hence to devise a load forecasting technique that can yield the best estimates on diverse datasets, specially when the training data is limited, is a big challenge. This paper presents a deep learning architecture for short-term load forecasting based on bidirectional sequential models in conjunction with feature engineering that extracts the hand-crafted derived features in order to aid the model for better learning and predictions. In the proposed architecture, named as Deep Derived Feature Fusion (DeepDeFF), the raw input and hand-crafted features are trained at separate levels and then their respective outputs are combined to make the final prediction. The efficacy of the proposed methodology is evaluated on datasets from five countries with completely different patterns. The results demonstrate that the proposed technique is superior to the existing state of the art.

AFP-SRC: Identification of Antifreeze Proteins Using Sparse Representation Classifier

Species living in the extreme cold environment fight against the harsh conditions using antifreeze proteins (AFPs), that manipulates the freezing mechanism of water in more than one way. This amazing nature of AFP turns out to be extremely useful in several industrial and medical applications. The lack of similarity in their structure and sequence makes their prediction an arduous task and identifying them experimentally in the wet-lab is time-consuming and expensive. In this research, we propose a computational framework for the prediction of AFPs which is essentially based on a sample-specific classification method using the sparse reconstruction. A linear model and an over-complete dictionary matrix of known AFPs are used to predict a sparse class-label vector that provides a sample-association score. Delta-rule is applied for the reconstruction of two pseudo-samples using lower and upper parts of the sample-association vector and based on the minimum recovery score, class labels are assigned. We compare our approach with contemporary methods on a standard dataset and the proposed method is found to outperform in terms of Balanced accuracy and Youden's index. The MATLAB implementation of the proposed method is available at the author's GitHub page (\{https://github.com/Shujaat123/AFP-SRC}{https://github.com/Shujaat123/AFP-SRC}).

A Mathematical Framework for Deep Learning in Elastic Source Imaging

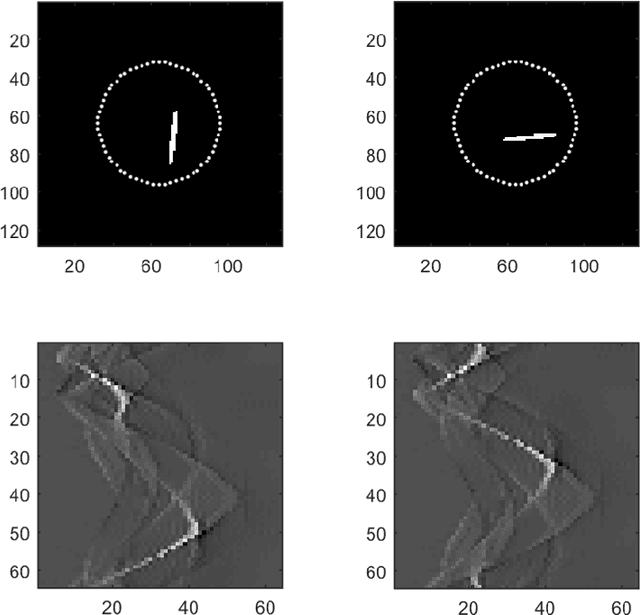
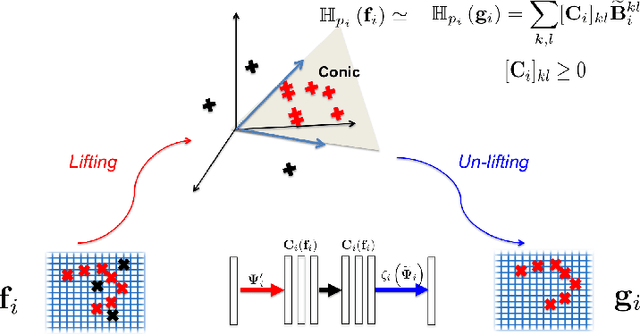
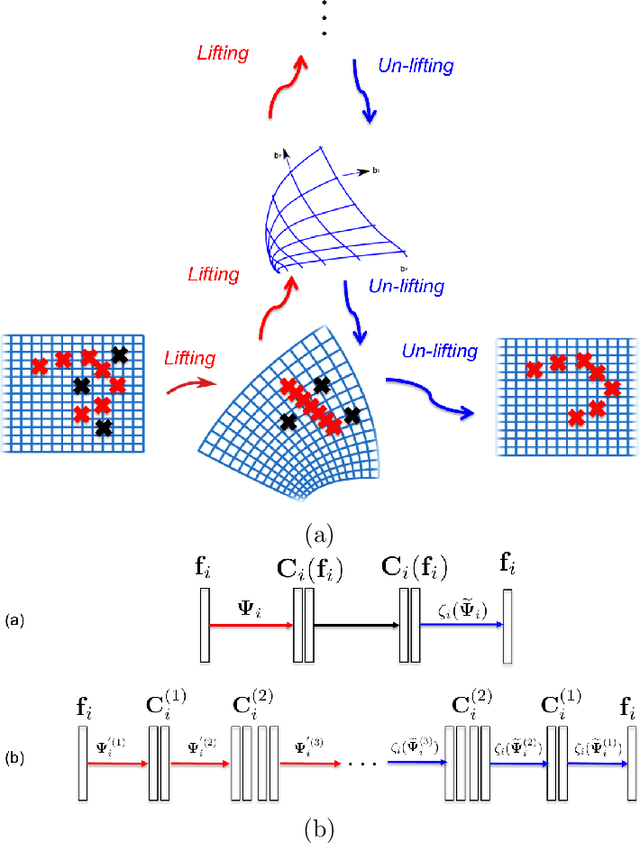
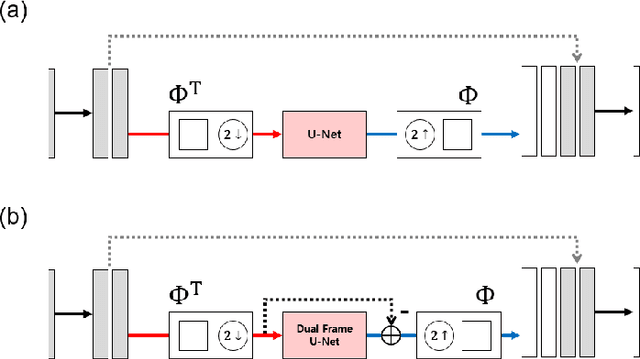
An inverse elastic source problem with sparse measurements is of concern. A generic mathematical framework is proposed which incorporates a low- dimensional manifold regularization in the conventional source reconstruction algorithms thereby enhancing their performance with sparse datasets. It is rigorously established that the proposed framework is equivalent to the so-called \emph{deep convolutional framelet expansion} in machine learning literature for inverse problems. Apposite numerical examples are furnished to substantiate the efficacy of the proposed framework.

Deep Learning Can Reverse Photon Migration for Diffuse Optical Tomography

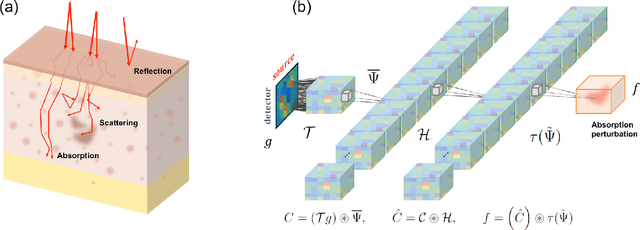
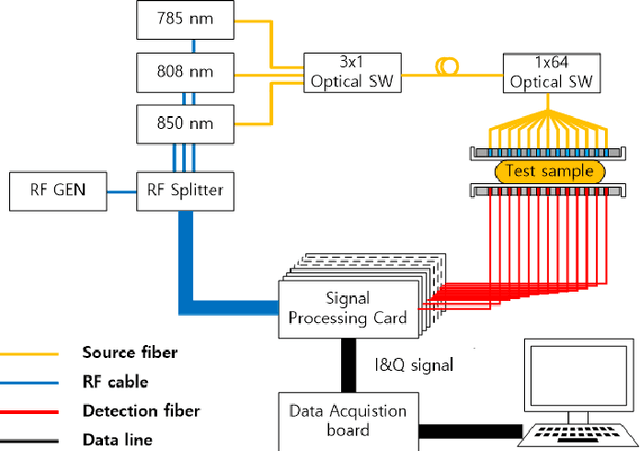
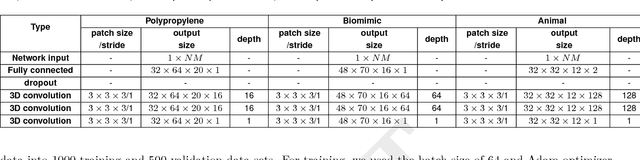
Can artificial intelligence (AI) learn complicated non-linear physics? Here we propose a novel deep learning approach that learns non-linear photon scattering physics and obtains accurate 3D distribution of optical anomalies. In contrast to the traditional black-box deep learning approaches to inverse problems, our deep network learns to invert the Lippmann-Schwinger integral equation which describes the essential physics of photon migration of diffuse near-infrared (NIR) photons in turbid media. As an example for clinical relevance, we applied the method to our prototype diffuse optical tomography (DOT). We show that our deep neural network, trained with only simulation data, can accurately recover the location of anomalies within biomimetic phantoms and live animals without the use of an exogenous contrast agent.