A Mathematical Framework for Deep Learning in Elastic Source Imaging
Paper and Code
May 25, 2018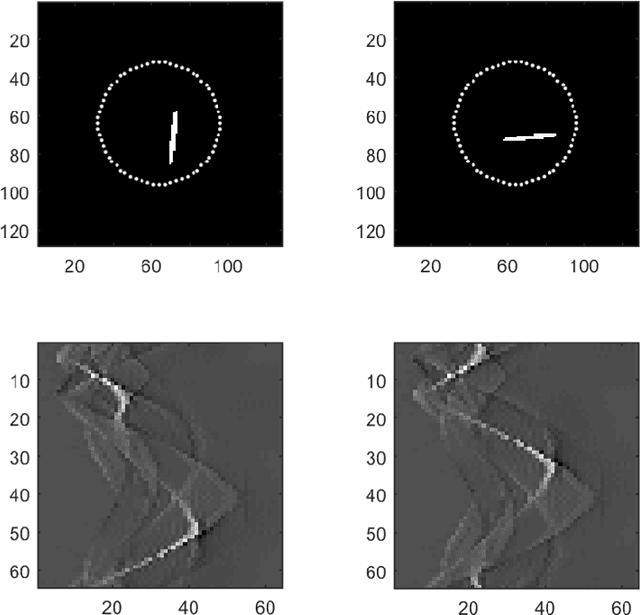
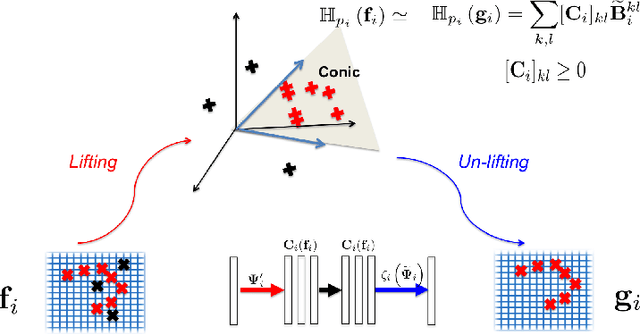
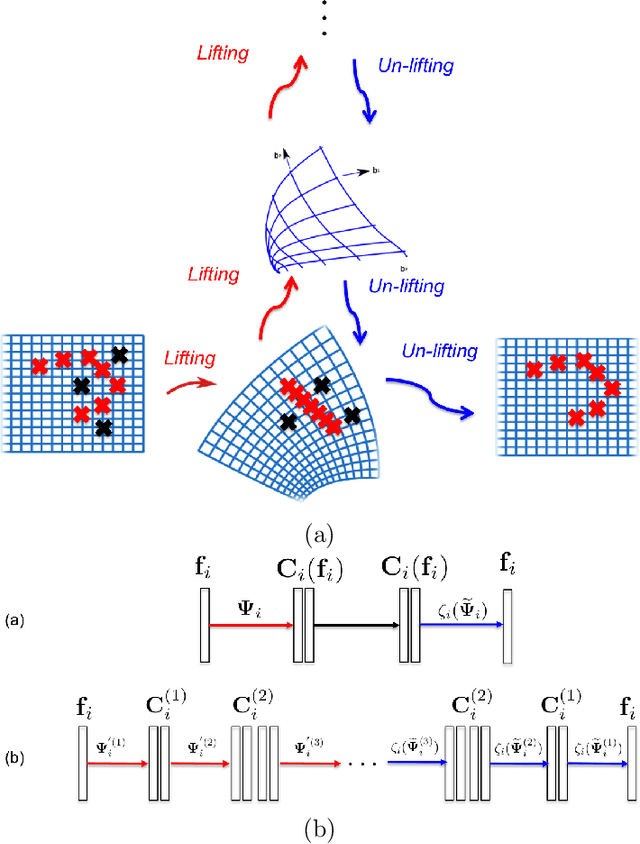
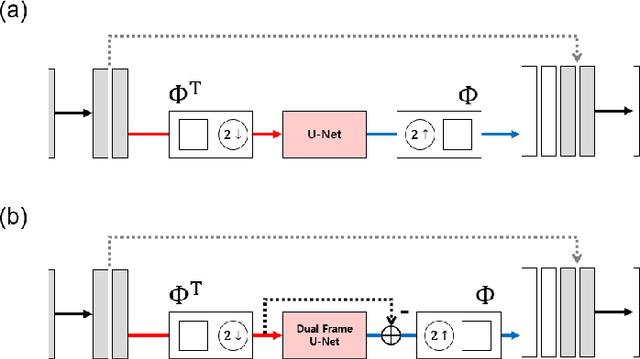
An inverse elastic source problem with sparse measurements is of concern. A generic mathematical framework is proposed which incorporates a low- dimensional manifold regularization in the conventional source reconstruction algorithms thereby enhancing their performance with sparse datasets. It is rigorously established that the proposed framework is equivalent to the so-called \emph{deep convolutional framelet expansion} in machine learning literature for inverse problems. Apposite numerical examples are furnished to substantiate the efficacy of the proposed framework.
* 28 pages, 14 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge