Multipolar Acoustic Source Reconstruction from Sparse Far-Field Data using ALOHA

The reconstruction of multipolar acoustic or electromagnetic sources from their far-field radiation patterns plays a crucial role in numerous practical applications. Most of the existing techniques for source reconstruction require dense multi-frequency data at the Nyquist sampling rate. Accessibility of only sparse data at a sub-sampled grid contributes to the null space of the inverse source-to-data operator, which causes significant imaging artifacts. For this purpose, additional knowledge about the source or regularization is required. In this article, we propose a novel two-stage strategy for multipolar source reconstruction from the sub-sampled sparse data that takes advantage of the sparsity of the sources in the physical domain. The data at the Nyquist sampling rate is recovered from sub-sampled data and then a conventional inversion algorithm is used to reconstruct sources. The data recovery problem is linked to a spectrum recovery problem for the signal with the finite rate of innovations (FIR) that is solved using an annihilating filter-based structured Hankel matrix completion approach (ALOHA). For an accurate reconstruction of multipolar sources, we employ a Fourier inversion algorithm. The suitability of the suggested approach for both noisy and noise-free measurements is supported by numerical evidence.

An inverse scattering approach for geometric body generation: a machine learning perspective

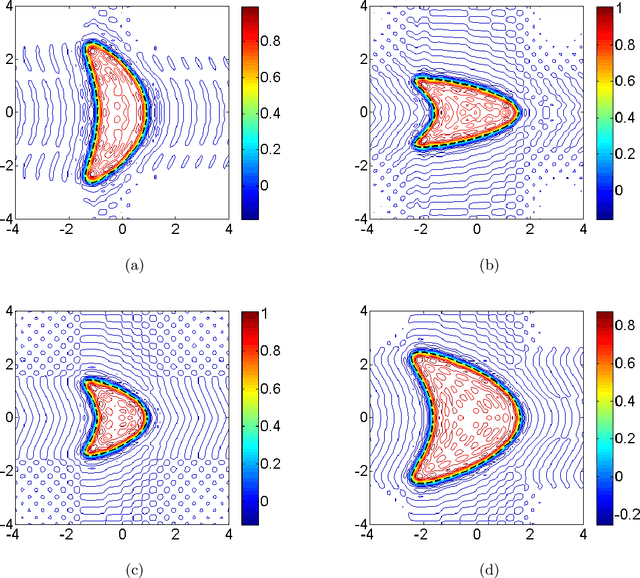
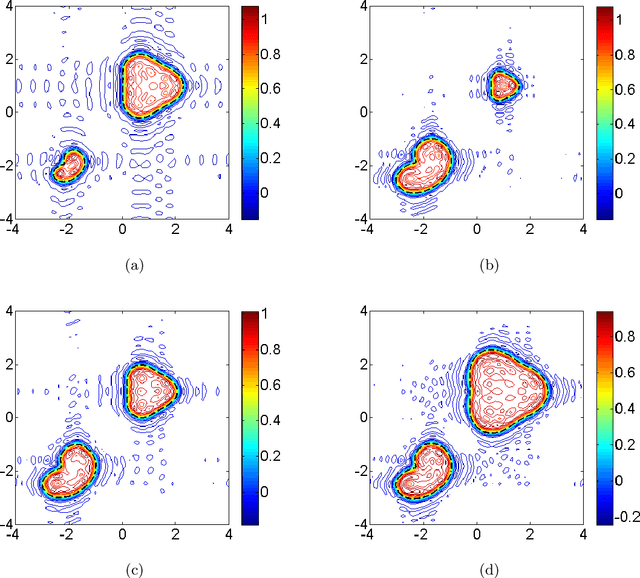
In this paper, we are concerned with the 2D and 3D geometric shape generation by prescribing a set of characteristic values of a specific geometric body. One of the major motivations of our study is the 3D human body generation in various applications. We develop a novel method that can generate the desired body with customized characteristic values. The proposed method follows a machine-learning flavour that generates the inferred geometric body with the input characteristic parameters from a training dataset. One of the critical ingredients and novelties of our method is the borrowing of inverse scattering techniques in the theory of wave propagation to the body generation. This is done by establishing a delicate one-to-one correspondence between a geometric body and the far-field pattern of a source scattering problem governed by the Helmholtz system. It in turn enables us to establish a one-to-one correspondence between the geometric body space and the function space defined by the far-field patterns. Hence, the far-field patterns can act as the shape generators. The shape generation with prescribed characteristic parameters is achieved by first manipulating the shape generators and then reconstructing the corresponding geometric body from the obtained shape generator by a stable multiple-frequency Fourier method. Our method is easy to implement and produces more efficient and stable body generations. We provide both theoretical analysis and extensive numerical experiments for the proposed method. The study is the first attempt to introduce inverse scattering approaches in combination with machine learning to the geometric body generation and it opens up many opportunities for further developments.