Anticancer Peptides Classification using Kernel Sparse Representation Classifier

Cancer is one of the most challenging diseases because of its complexity, variability, and diversity of causes. It has been one of the major research topics over the past decades, yet it is still poorly understood. To this end, multifaceted therapeutic frameworks are indispensable. \emph{Anticancer peptides} (ACPs) are the most promising treatment option, but their large-scale identification and synthesis require reliable prediction methods, which is still a problem. In this paper, we present an intuitive classification strategy that differs from the traditional \emph{black box} method and is based on the well-known statistical theory of \emph{sparse-representation classification} (SRC). Specifically, we create over-complete dictionary matrices by embedding the \emph{composition of the K-spaced amino acid pairs} (CKSAAP). Unlike the traditional SRC frameworks, we use an efficient \emph{matching pursuit} solver instead of the computationally expensive \emph{basis pursuit} solver in this strategy. Furthermore, the \emph{kernel principal component analysis} (KPCA) is employed to cope with non-linearity and dimension reduction of the feature space whereas the \emph{synthetic minority oversampling technique} (SMOTE) is used to balance the dictionary. The proposed method is evaluated on two benchmark datasets for well-known statistical parameters and is found to outperform the existing methods. The results show the highest sensitivity with the most balanced accuracy, which might be beneficial in understanding structural and chemical aspects and developing new ACPs. The Google-Colab implementation of the proposed method is available at the author's GitHub page (\href{https://github.com/ehtisham-Fazal/ACP-Kernel-SRC}{https://github.com/ehtisham-fazal/ACP-Kernel-SRC}).

Performance Analysis of Fractional Learning Algorithms

Fractional learning algorithms are trending in signal processing and adaptive filtering recently. However, it is unclear whether the proclaimed superiority over conventional algorithms is well-grounded or is a myth as their performance has never been extensively analyzed. In this article, a rigorous analysis of fractional variants of the least mean squares and steepest descent algorithms is performed. Some critical schematic kinks in fractional learning algorithms are identified. Their origins and consequences on the performance of the learning algorithms are discussed and swift ready-witted remedies are proposed. Apposite numerical experiments are conducted to discuss the convergence and efficiency of the fractional learning algorithms in stochastic environments.

q-RBFNN:A Quantum Calculus-based RBF Neural Network

In this research a novel stochastic gradient descent based learning approach for the radial basis function neural networks (RBFNN) is proposed. The proposed method is based on the q-gradient which is also known as Jackson derivative. In contrast to the conventional gradient, which finds the tangent, the q-gradient finds the secant of the function and takes larger steps towards the optimal solution. The proposed $q$-RBFNN is analyzed for its convergence performance in the context of least square algorithm. In particular, a closed form expression of the Wiener solution is obtained, and stability bounds of the learning rate (step-size) is derived. The analytical results are validated through computer simulation. Additionally, we propose an adaptive technique for the time-varying $q$-parameter to improve convergence speed with no trade-offs in the steady state performance.

Multi-Kernel Fusion for RBF Neural Networks

A simple yet effective architectural design of radial basis function neural networks (RBFNN) makes them amongst the most popular conventional neural networks. The current generation of radial basis function neural network is equipped with multiple kernels which provide significant performance benefits compared to the previous generation using only a single kernel. In existing multi-kernel RBF algorithms, multi-kernel is formed by the convex combination of the base/primary kernels. In this paper, we propose a novel multi-kernel RBFNN in which every base kernel has its own (local) weight. This novel flexibility in the network provides better performance such as faster convergence rate, better local minima and resilience against stucking in poor local minima. These performance gains are achieved at a competitive computational complexity compared to the contemporary multi-kernel RBF algorithms. The proposed algorithm is thoroughly analysed for performance gain using mathematical and graphical illustrations and also evaluated on three different types of problems namely: (i) pattern classification, (ii) system identification and (iii) function approximation. Empirical results clearly show the superiority of the proposed algorithm compared to the existing state-of-the-art multi-kernel approaches.

Heart Segmentation From MRI Scans Using Convolutional Neural Network

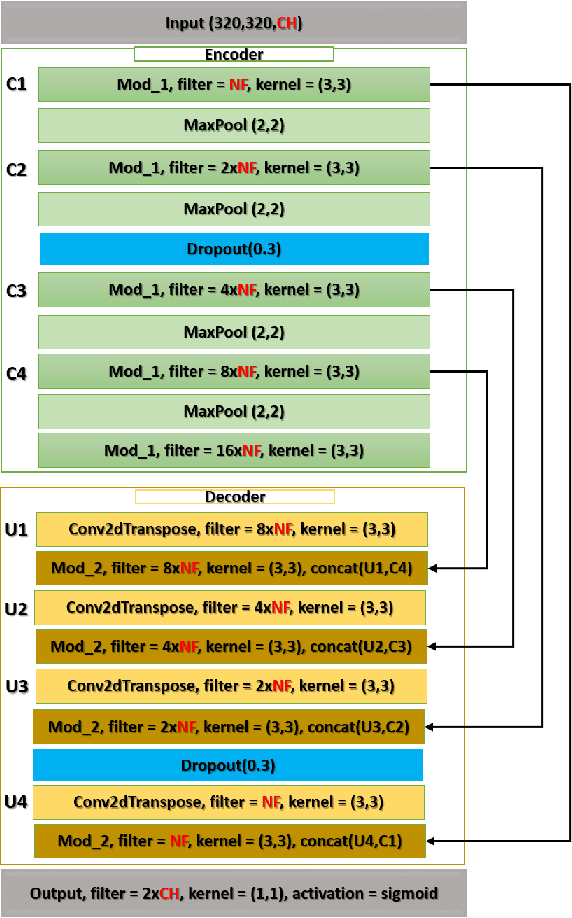
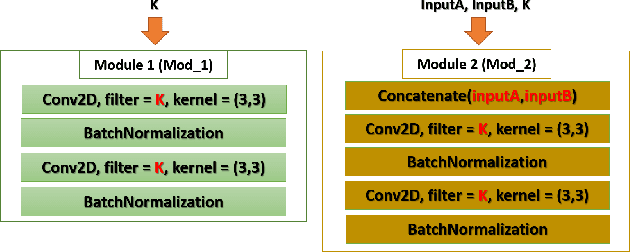
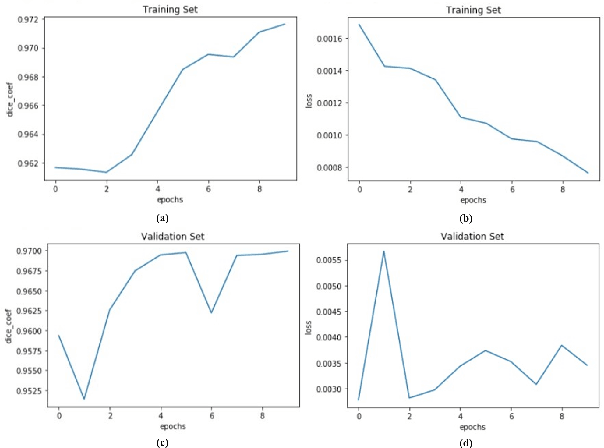
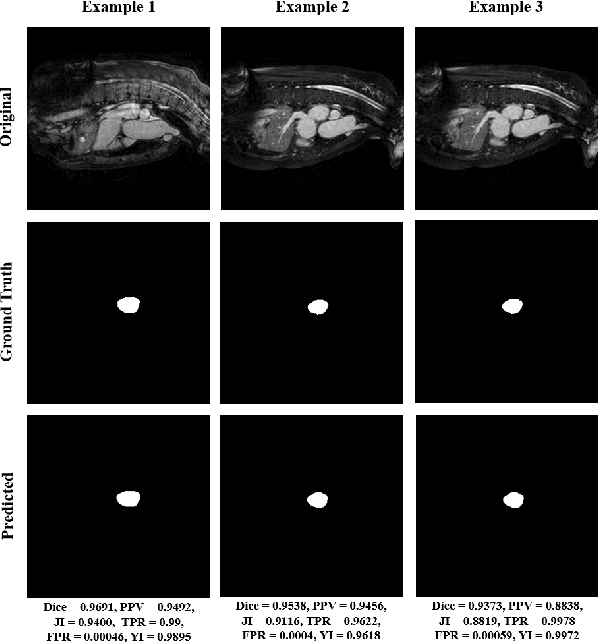
Heart is one of the vital organs of human body. A minor dysfunction of heart even for a short time interval can be fatal, therefore, efficient monitoring of its physiological state is essential for the patients with cardiovascular diseases. In the recent past, various computer assisted medical imaging systems have been proposed for the segmentation of the organ of interest. However, for the segmentation of heart using MRI, only few methods have been proposed each with its own merits and demerits. For further advancement in this area of research, we analyze automated heart segmentation methods for magnetic resonance images. The analysis are based on deep learning methods that processes a full MR scan in a slice by slice fashion to predict desired mask for heart region. We design two encoder decoder type fully convolutional neural network models

Spatio-Temporal RBF Neural Networks

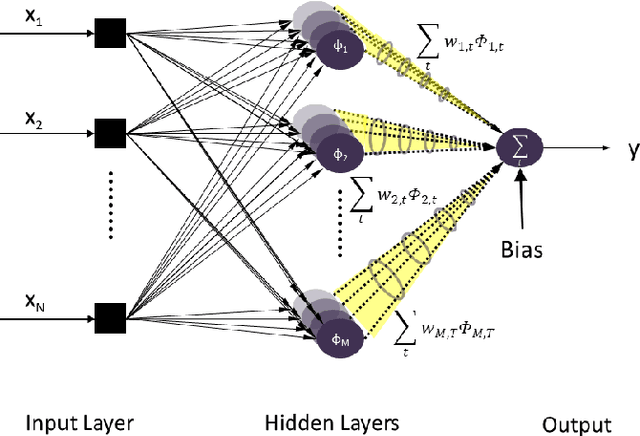
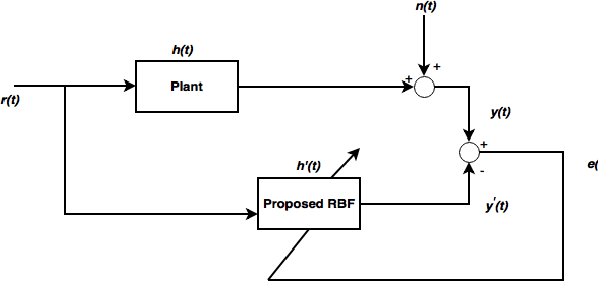
Herein, we propose a spatio-temporal extension of RBFNN for nonlinear system identification problem. The proposed algorithm employs the concept of time-space orthogonality and separately models the dynamics and nonlinear complexities of the system. The proposed RBF architecture is explored for the estimation of a highly nonlinear system and results are compared with the standard architecture for both the conventional and fractional gradient decent-based learning rules. The spatio-temporal RBF is shown to perform better than the standard and fractional RBFNNs by achieving fast convergence and significantly reduced estimation error.

A Novel Adaptive Kernel for the RBF Neural Networks

In this paper, we propose a novel adaptive kernel for the radial basis function (RBF) neural networks. The proposed kernel adaptively fuses the Euclidean and cosine distance measures to exploit the reciprocating properties of the two. The proposed framework dynamically adapts the weights of the participating kernels using the gradient descent method thereby alleviating the need for predetermined weights. The proposed method is shown to outperform the manual fusion of the kernels on three major problems of estimation namely nonlinear system identification, pattern classification and function approximation.

q-LMF: Quantum Calculus-based Least Mean Fourth Algorithm

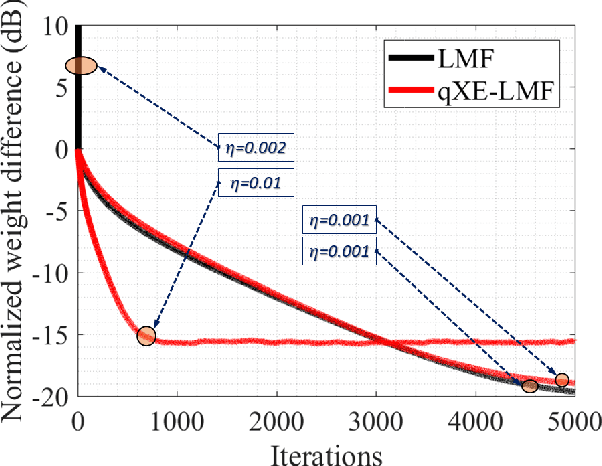
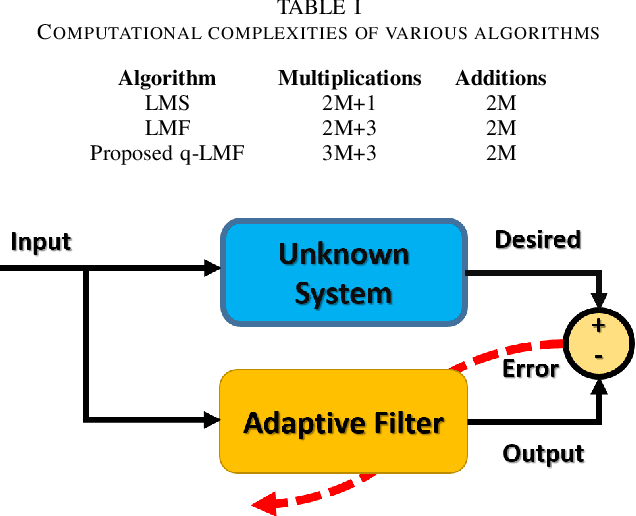
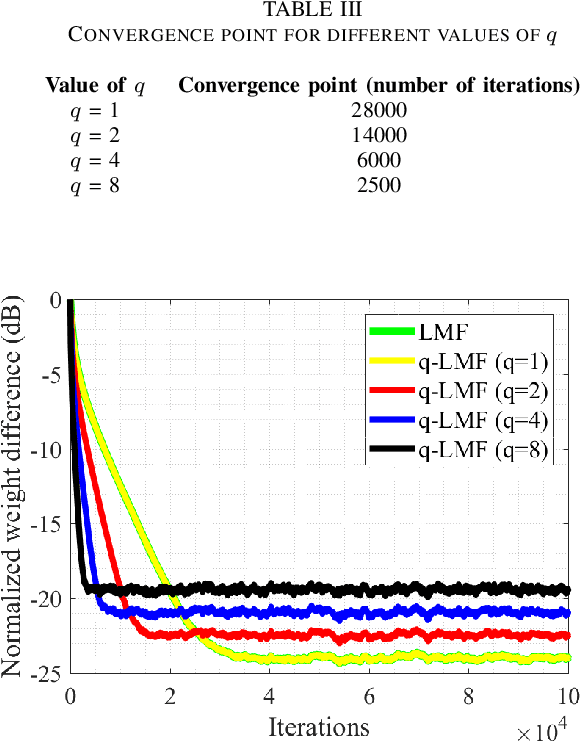
Channel estimation is an essential part of modern communication systems as it enhances the overall performance of the system. In recent past a variety of adaptive learning methods have been designed to enhance the robustness and convergence speed of the learning process. However, the need for an optimal technique is still there. Herein, for non-Gaussian noisy environment we propose a new class of stochastic gradient algorithm for channel identification. The proposed $q$-least mean fourth ($q$-LMF) is an extension of least mean fourth (LMF) algorithm and it is based on the $q$-calculus which is also known as Jackson derivative. The proposed algorithm utilizes a novel concept of error-correlation energy and normalization of signal to ensure high convergence rate, better stability and low steady-state error. Contrary to the conventional LMF, the proposed method has more freedom for large step-sizes. Extensive experiments show significant gain in the performance of the proposed $q$-LMF algorithm in comparison to the contemporary techniques.

RAFP-Pred: Robust Prediction of Antifreeze Proteins using Localized Analysis of n-Peptide Compositions

In extreme cold weather, living organisms produce Antifreeze Proteins (AFPs) to counter the otherwise lethal intracellular formation of ice. Structures and sequences of various AFPs exhibit a high degree of heterogeneity, consequently the prediction of the AFPs is considered to be a challenging task. In this research, we propose to handle this arduous manifold learning task using the notion of localized processing. In particular an AFP sequence is segmented into two sub-segments each of which is analyzed for amino acid and di-peptide compositions. We propose to use only the most significant features using the concept of information gain (IG) followed by a random forest classification approach. The proposed RAFP-Pred achieved an excellent performance on a number of standard datasets. We report a high Youden's index (sensitivity+specificity-1) value of 0.75 on the standard independent test data set outperforming the AFP-PseAAC, AFP\_PSSM, AFP-Pred and iAFP by a margin of 0.05, 0.06, 0.14 and 0.68 respectively. The verification rate on the UniProKB dataset is found to be 83.19\% which is substantially superior to the 57.18\% reported for the iAFP method.

Comments on "Momentum fractional LMS for power signal parameter estimation"

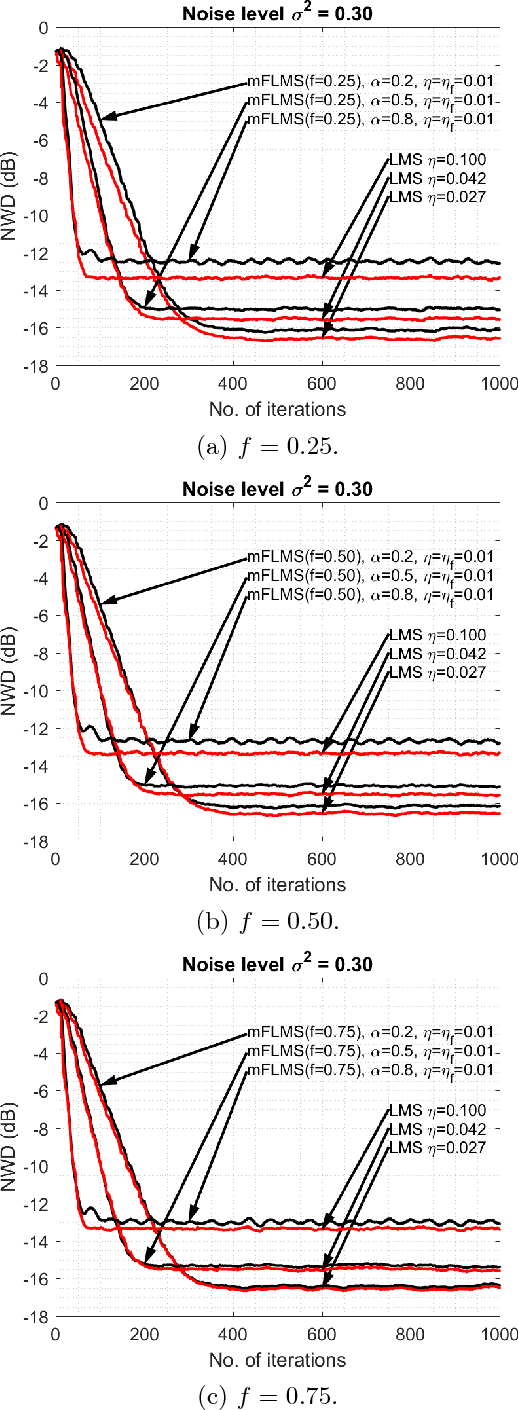
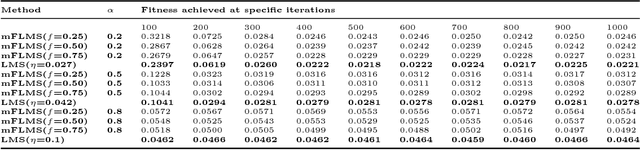
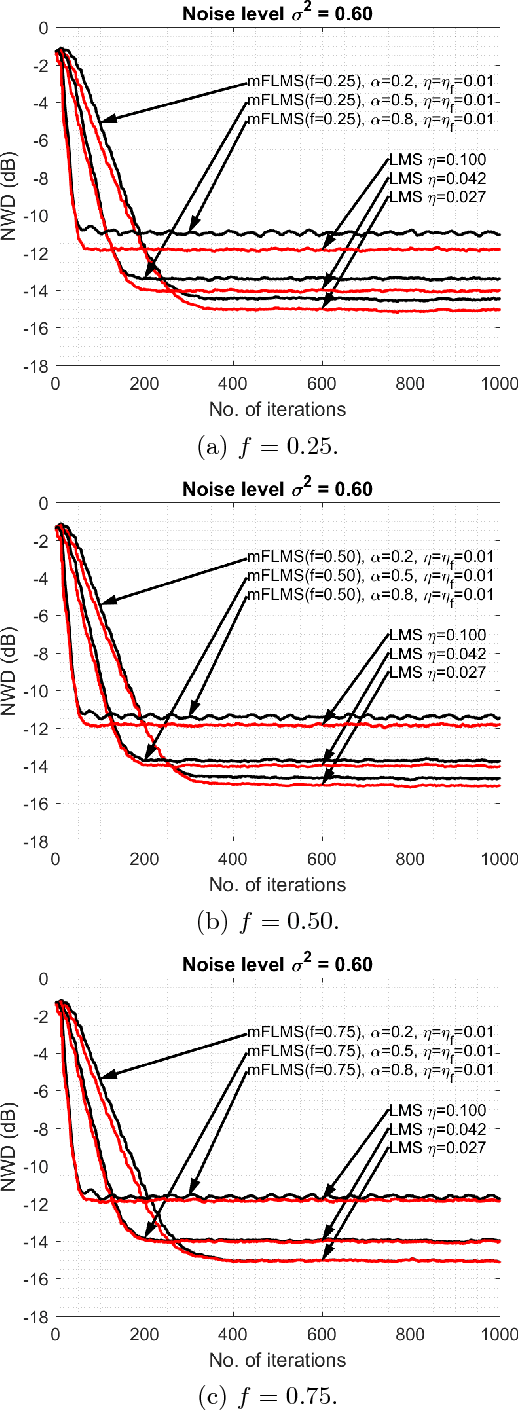
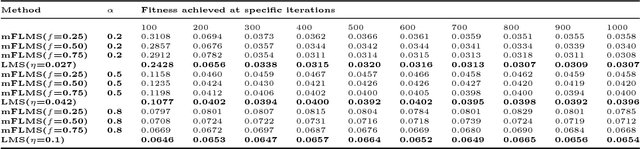
The purpose of this paper is to indicate that the recently proposed Momentum fractional least mean squares (mFLMS) algorithm has some serious flaws in its design and analysis. Our apprehensions are based on the evidence we found in the derivation and analysis in the paper titled: \textquotedblleft \textit{Momentum fractional LMS for power signal parameter estimation}\textquotedblright. In addition to the theoretical bases our claims are also verified through extensive simulation results. The experiments clearly show that the new method does not have any advantage over the classical least mean square (LMS) method.