Muhammad Moinuddin
Regularized Linear Discriminant Analysis Using a Nonlinear Covariance Matrix Estimator
Feb 07, 2024



Abstract:Linear discriminant analysis (LDA) is a widely used technique for data classification. The method offers adequate performance in many classification problems, but it becomes inefficient when the data covariance matrix is ill-conditioned. This often occurs when the feature space's dimensionality is higher than or comparable to the training data size. Regularized LDA (RLDA) methods based on regularized linear estimators of the data covariance matrix have been proposed to cope with such a situation. The performance of RLDA methods is well studied, with optimal regularization schemes already proposed. In this paper, we investigate the capability of a positive semidefinite ridge-type estimator of the inverse covariance matrix that coincides with a nonlinear (NL) covariance matrix estimator. The estimator is derived by reformulating the score function of the optimal classifier utilizing linear estimation methods, which eventually results in the proposed NL-RLDA classifier. We derive asymptotic and consistent estimators of the proposed technique's misclassification rate under the assumptions of a double-asymptotic regime and multivariate Gaussian model for the classes. The consistent estimator, coupled with a one-dimensional grid search, is used to set the value of the regularization parameter required for the proposed NL-RLDA classifier. Performance evaluations based on both synthetic and real data demonstrate the effectiveness of the proposed classifier. The proposed technique outperforms state-of-art methods over multiple datasets. When compared to state-of-the-art methods across various datasets, the proposed technique exhibits superior performance.
Portfolio Optimization Using a Consistent Vector-Based MSE Estimation Approach
Apr 12, 2022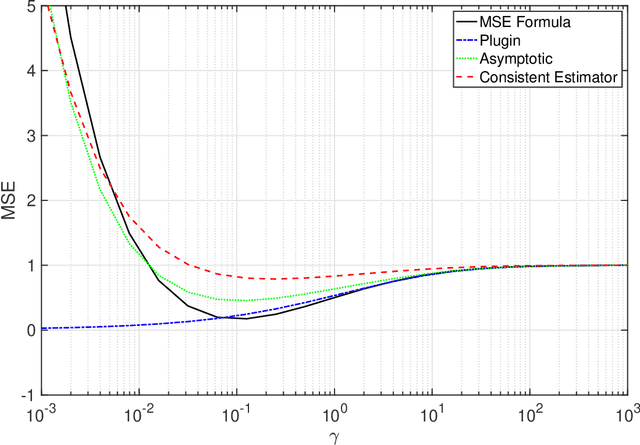
Abstract:This paper is concerned with optimizing the global minimum-variance portfolio's (GMVP) weights in high-dimensional settings where both observation and population dimensions grow at a bounded ratio. Optimizing the GMVP weights is highly influenced by the data covariance matrix estimation. In a high-dimensional setting, it is well known that the sample covariance matrix is not a proper estimator of the true covariance matrix since it is not invertible when we have fewer observations than the data dimension. Even with more observations, the sample covariance matrix may not be well-conditioned. This paper determines the GMVP weights based on a regularized covariance matrix estimator to overcome the aforementioned difficulties. Unlike other methods, the proper selection of the regularization parameter is achieved by minimizing the mean-squared error of an estimate of the noise vector that accounts for the uncertainty in the data mean estimation. Using random-matrix-theory tools, we derive a consistent estimator of the achievable mean-squared error that allows us to find the optimal regularization parameter using a simple line search. Simulation results demonstrate the effectiveness of the proposed method when the data dimension is larger than the number of data samples or of the same order.
Mean-square Analysis of the NLMS Algorithm
Aug 08, 2021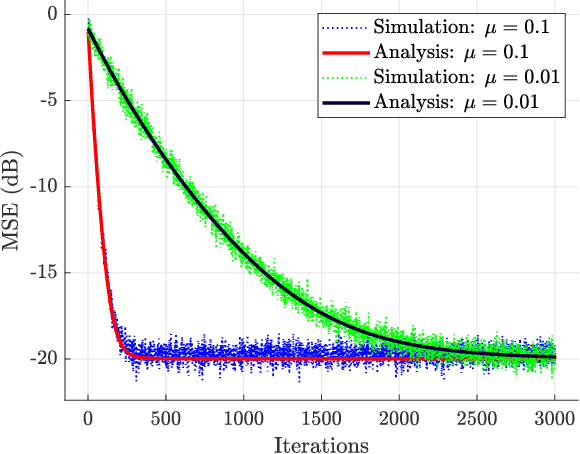


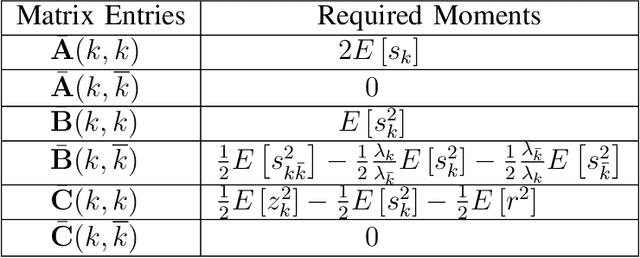
Abstract:This work presents a novel approach to the mean-square analysis of the normalized least mean squares (NLMS) algorithm for circular complex colored Gaussian inputs. The analysis is based on the derivation of a closed-form expression for the Cumulative Distribution Function (CDF) of random variables of the form $(||{\bf u}||_{{\bf D}_1}^2)(||{\bf u}||_{{\bf D}_2}^2)^{-1}$ where ${\bf u}$ is an isotropic vector and ${\bf D}_1$ and ${\bf D}_2$ are diagonal matrices and using that to derive some moments of these variables. These moments in turn completely characterize the mean-square behavior of the NLMS algorithm in explicit closed-form expressions. Specifically, the transient, steady-state, and tracking mean-square behavior of the NLMS algorithm is studied.
Heart Segmentation From MRI Scans Using Convolutional Neural Network
Nov 21, 2019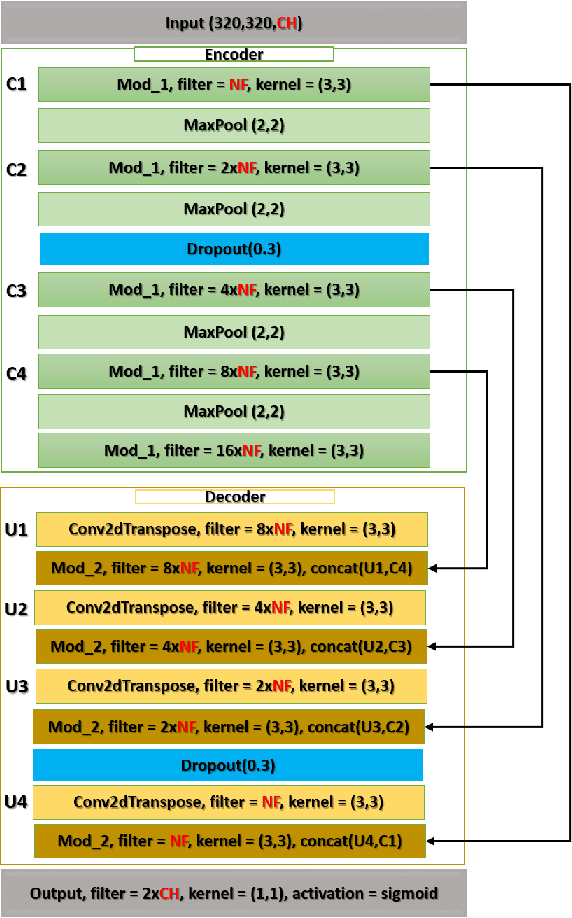
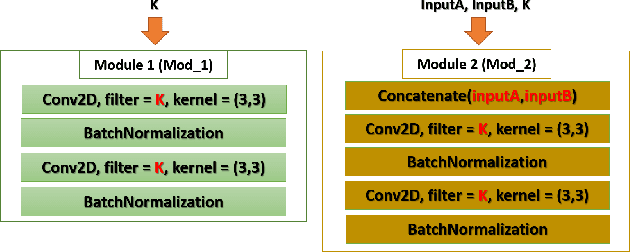
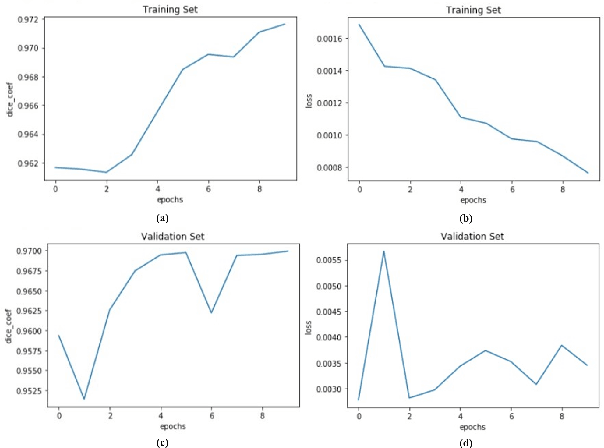
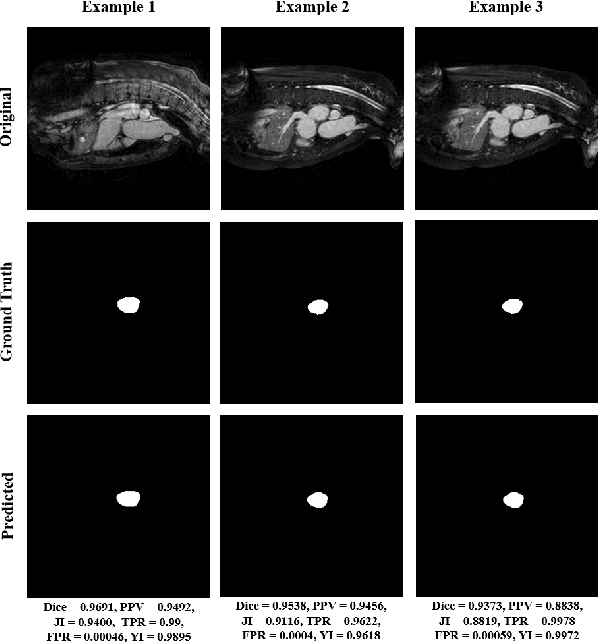
Abstract:Heart is one of the vital organs of human body. A minor dysfunction of heart even for a short time interval can be fatal, therefore, efficient monitoring of its physiological state is essential for the patients with cardiovascular diseases. In the recent past, various computer assisted medical imaging systems have been proposed for the segmentation of the organ of interest. However, for the segmentation of heart using MRI, only few methods have been proposed each with its own merits and demerits. For further advancement in this area of research, we analyze automated heart segmentation methods for magnetic resonance images. The analysis are based on deep learning methods that processes a full MR scan in a slice by slice fashion to predict desired mask for heart region. We design two encoder decoder type fully convolutional neural network models
Spatio-Temporal RBF Neural Networks
Aug 04, 2019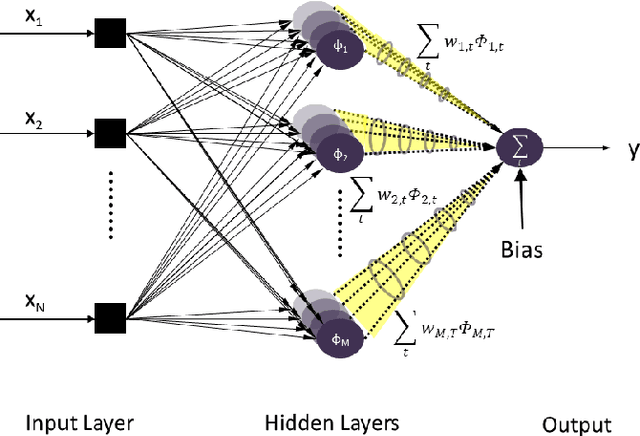
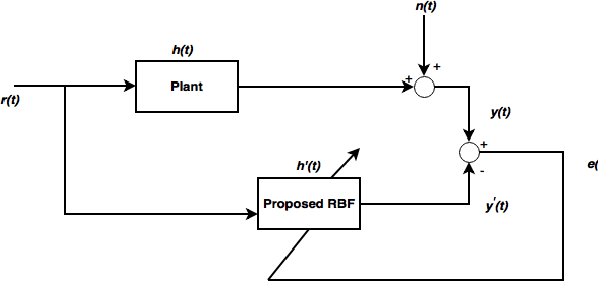

Abstract:Herein, we propose a spatio-temporal extension of RBFNN for nonlinear system identification problem. The proposed algorithm employs the concept of time-space orthogonality and separately models the dynamics and nonlinear complexities of the system. The proposed RBF architecture is explored for the estimation of a highly nonlinear system and results are compared with the standard architecture for both the conventional and fractional gradient decent-based learning rules. The spatio-temporal RBF is shown to perform better than the standard and fractional RBFNNs by achieving fast convergence and significantly reduced estimation error.
* Published in 2018 3rd International Conference on Emerging Trends in Engineering, Sciences and Technology (ICEEST)
q-LMF: Quantum Calculus-based Least Mean Fourth Algorithm
Dec 20, 2018
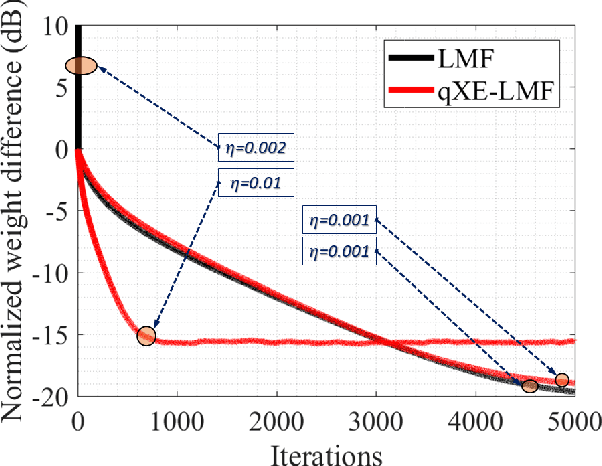
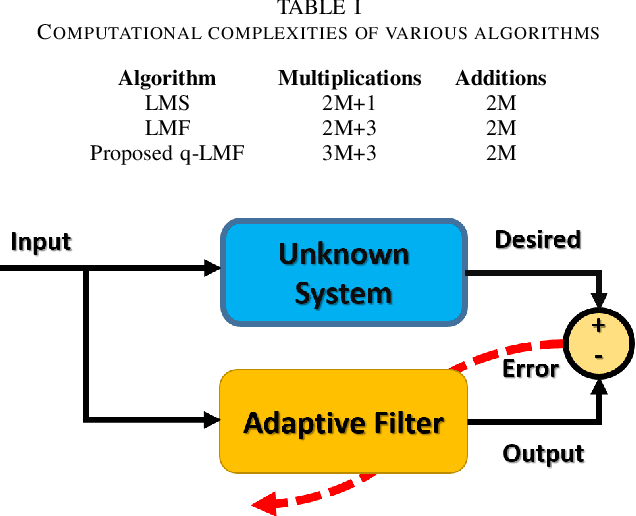
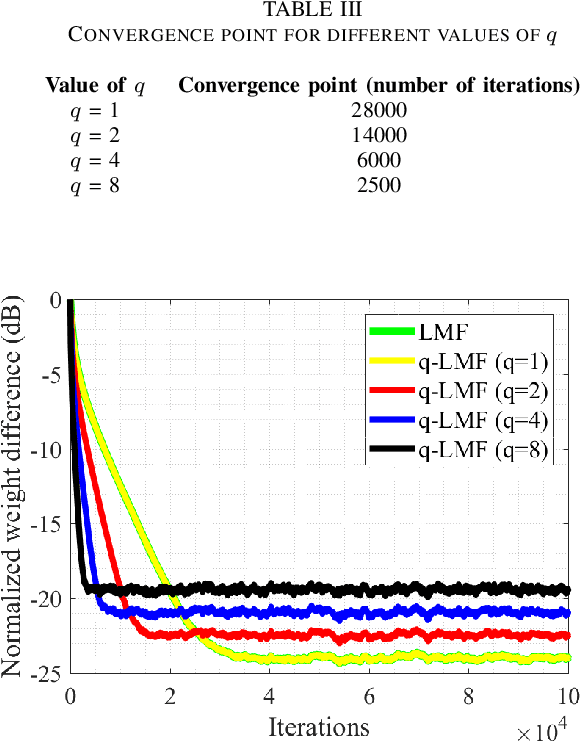
Abstract:Channel estimation is an essential part of modern communication systems as it enhances the overall performance of the system. In recent past a variety of adaptive learning methods have been designed to enhance the robustness and convergence speed of the learning process. However, the need for an optimal technique is still there. Herein, for non-Gaussian noisy environment we propose a new class of stochastic gradient algorithm for channel identification. The proposed $q$-least mean fourth ($q$-LMF) is an extension of least mean fourth (LMF) algorithm and it is based on the $q$-calculus which is also known as Jackson derivative. The proposed algorithm utilizes a novel concept of error-correlation energy and normalization of signal to ensure high convergence rate, better stability and low steady-state error. Contrary to the conventional LMF, the proposed method has more freedom for large step-sizes. Extensive experiments show significant gain in the performance of the proposed $q$-LMF algorithm in comparison to the contemporary techniques.
Comments on "Momentum fractional LMS for power signal parameter estimation"
May 19, 2018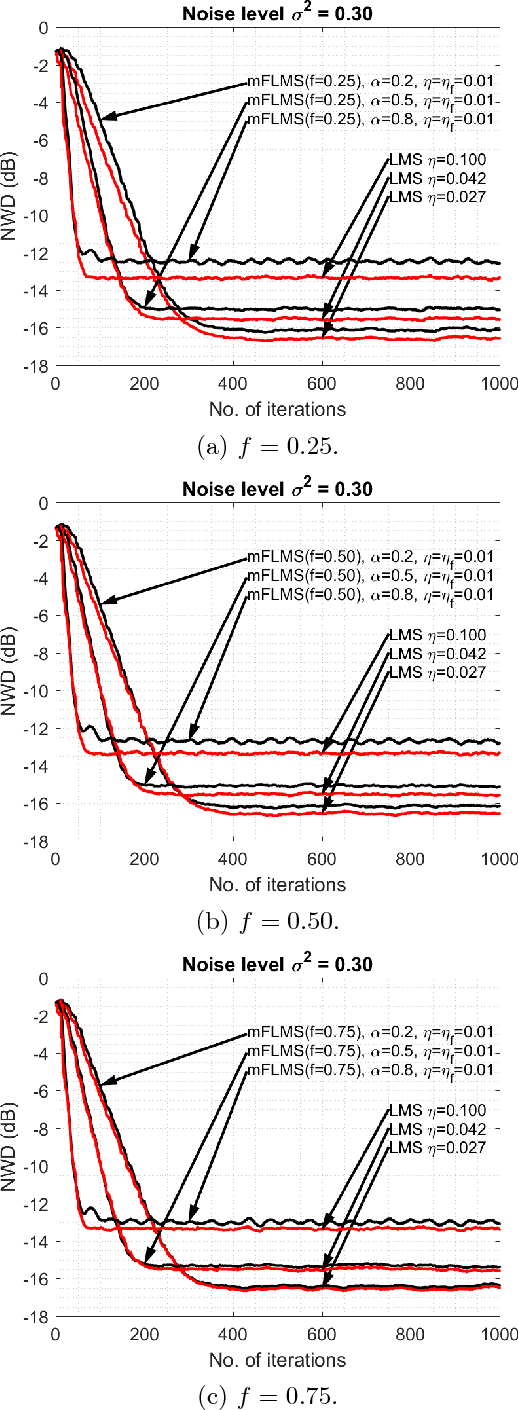
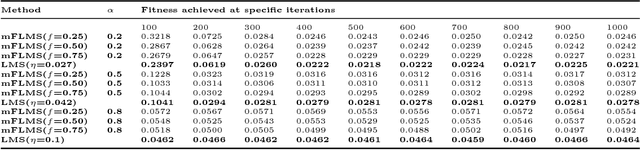
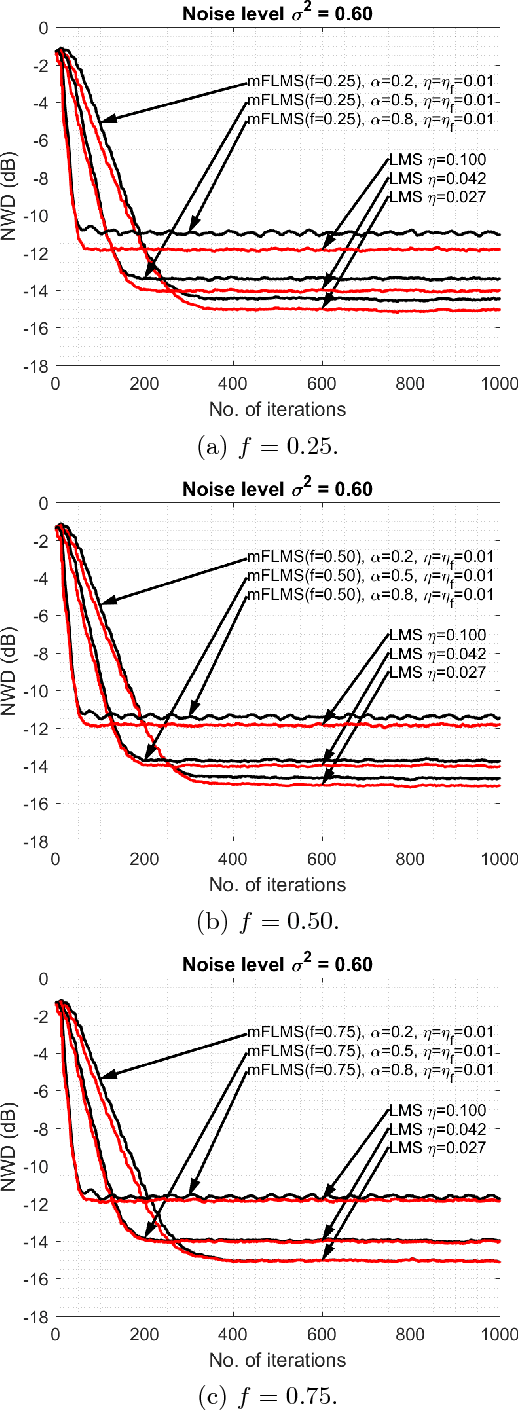
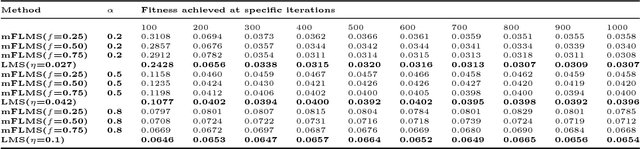
Abstract:The purpose of this paper is to indicate that the recently proposed Momentum fractional least mean squares (mFLMS) algorithm has some serious flaws in its design and analysis. Our apprehensions are based on the evidence we found in the derivation and analysis in the paper titled: \textquotedblleft \textit{Momentum fractional LMS for power signal parameter estimation}\textquotedblright. In addition to the theoretical bases our claims are also verified through extensive simulation results. The experiments clearly show that the new method does not have any advantage over the classical least mean square (LMS) method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge