Mean-square Analysis of the NLMS Algorithm
Paper and Code
Aug 08, 2021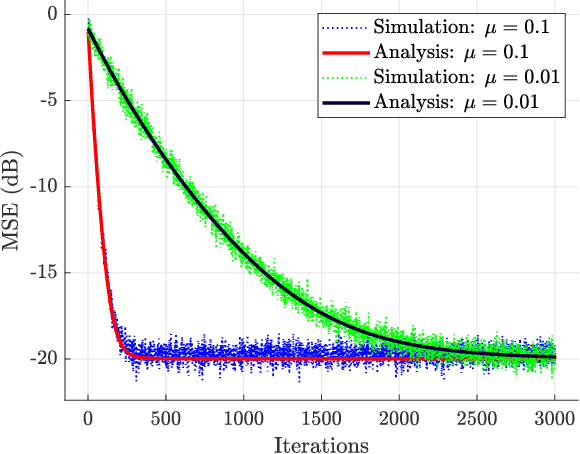


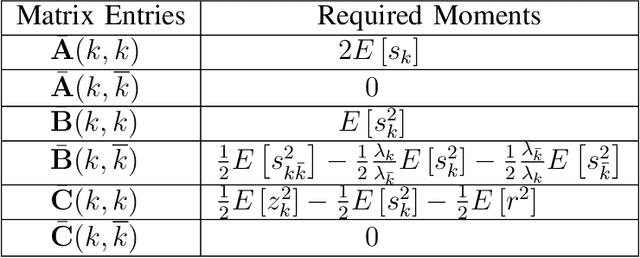
This work presents a novel approach to the mean-square analysis of the normalized least mean squares (NLMS) algorithm for circular complex colored Gaussian inputs. The analysis is based on the derivation of a closed-form expression for the Cumulative Distribution Function (CDF) of random variables of the form $(||{\bf u}||_{{\bf D}_1}^2)(||{\bf u}||_{{\bf D}_2}^2)^{-1}$ where ${\bf u}$ is an isotropic vector and ${\bf D}_1$ and ${\bf D}_2$ are diagonal matrices and using that to derive some moments of these variables. These moments in turn completely characterize the mean-square behavior of the NLMS algorithm in explicit closed-form expressions. Specifically, the transient, steady-state, and tracking mean-square behavior of the NLMS algorithm is studied.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge