Spatio-Temporal RBF Neural Networks

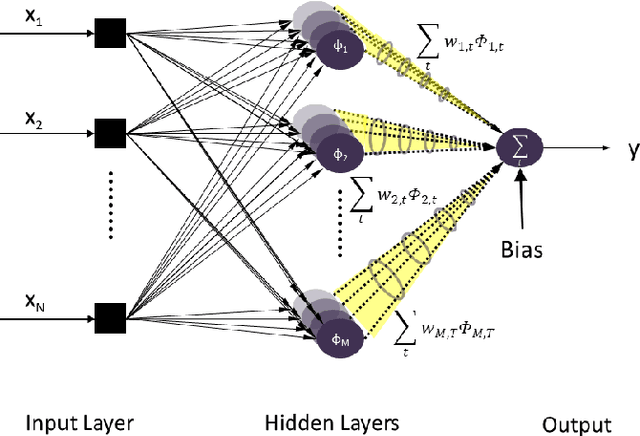
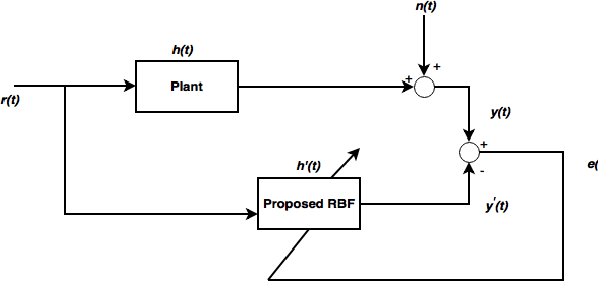
Herein, we propose a spatio-temporal extension of RBFNN for nonlinear system identification problem. The proposed algorithm employs the concept of time-space orthogonality and separately models the dynamics and nonlinear complexities of the system. The proposed RBF architecture is explored for the estimation of a highly nonlinear system and results are compared with the standard architecture for both the conventional and fractional gradient decent-based learning rules. The spatio-temporal RBF is shown to perform better than the standard and fractional RBFNNs by achieving fast convergence and significantly reduced estimation error.

Comments on "Momentum fractional LMS for power signal parameter estimation"

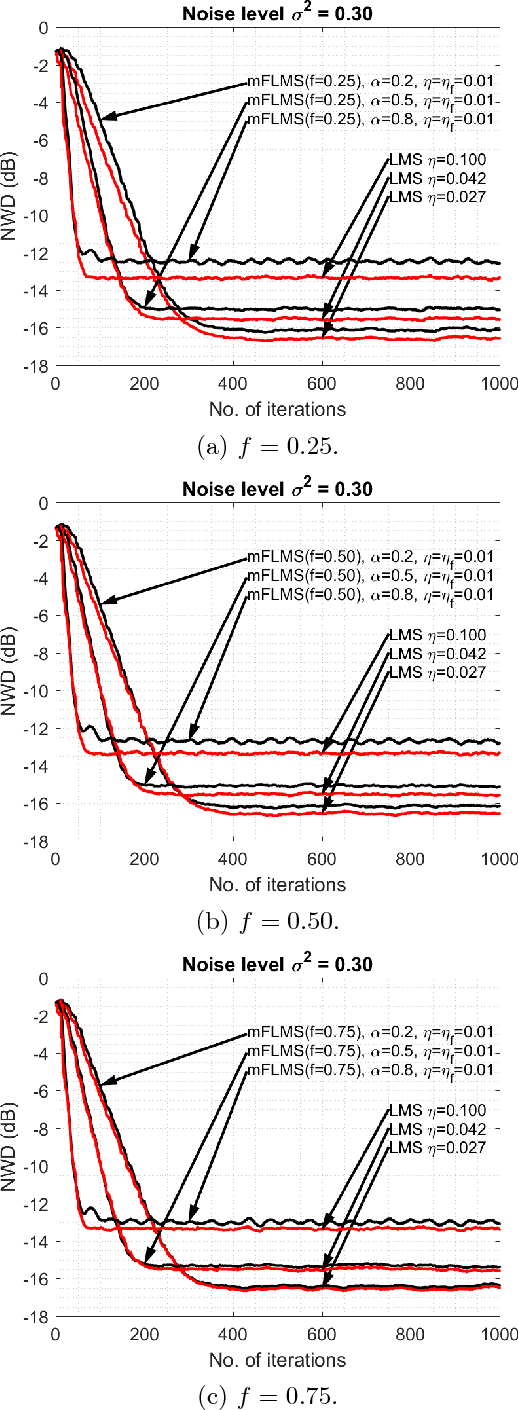
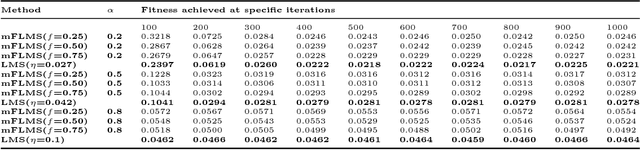
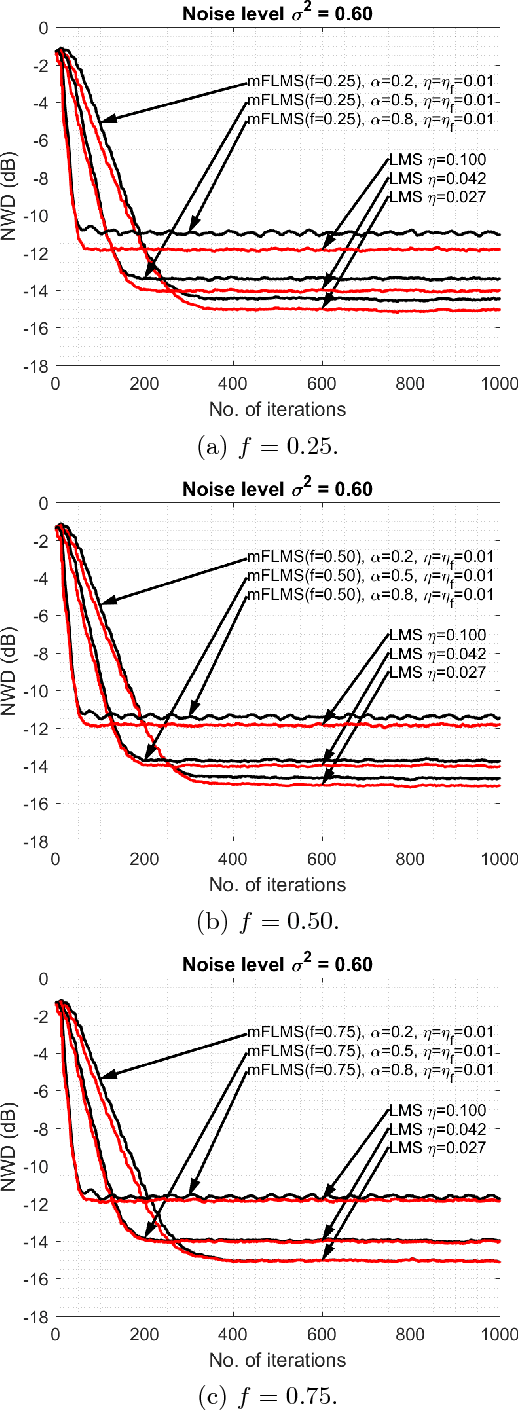
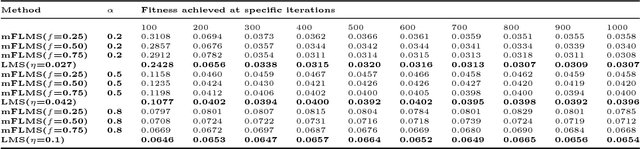
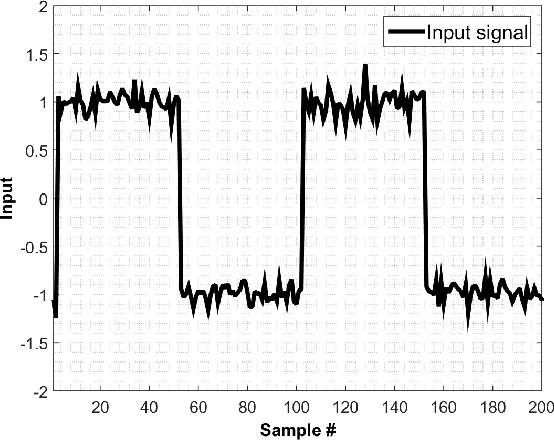
The purpose of this paper is to indicate that the recently proposed Momentum fractional least mean squares (mFLMS) algorithm has some serious flaws in its design and analysis. Our apprehensions are based on the evidence we found in the derivation and analysis in the paper titled: \textquotedblleft \textit{Momentum fractional LMS for power signal parameter estimation}\textquotedblright. In addition to the theoretical bases our claims are also verified through extensive simulation results. The experiments clearly show that the new method does not have any advantage over the classical least mean square (LMS) method.