q-LMF: Quantum Calculus-based Least Mean Fourth Algorithm
Paper and Code
Dec 20, 2018
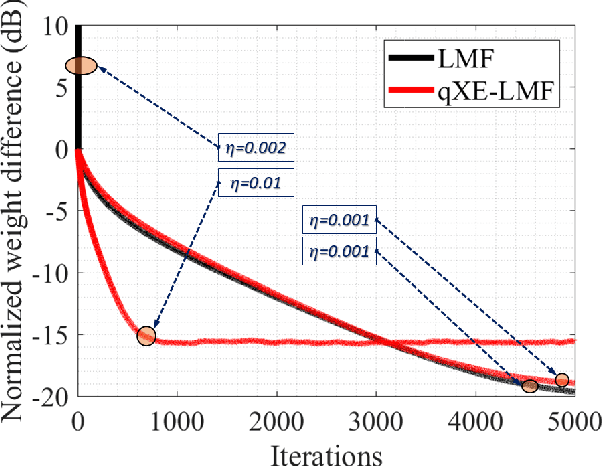
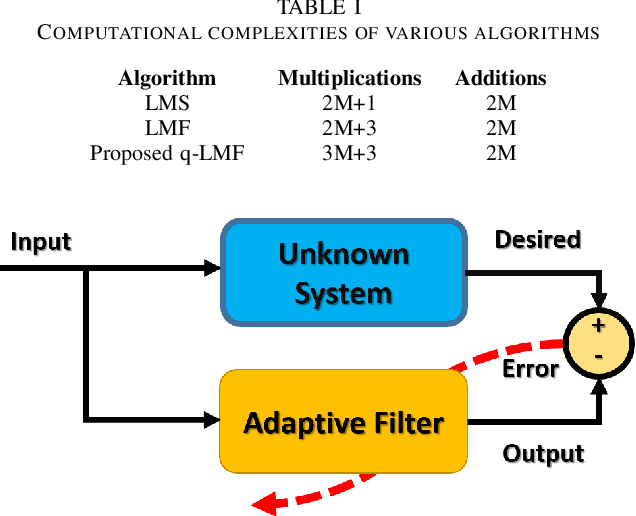
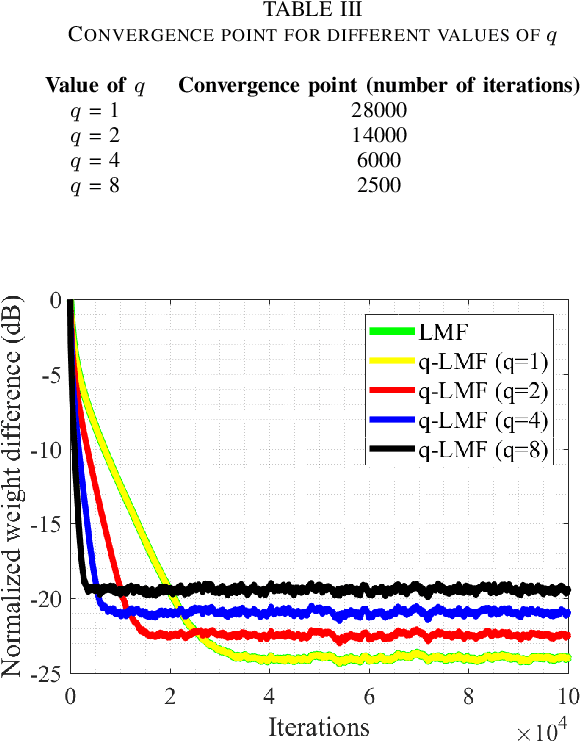
Channel estimation is an essential part of modern communication systems as it enhances the overall performance of the system. In recent past a variety of adaptive learning methods have been designed to enhance the robustness and convergence speed of the learning process. However, the need for an optimal technique is still there. Herein, for non-Gaussian noisy environment we propose a new class of stochastic gradient algorithm for channel identification. The proposed $q$-least mean fourth ($q$-LMF) is an extension of least mean fourth (LMF) algorithm and it is based on the $q$-calculus which is also known as Jackson derivative. The proposed algorithm utilizes a novel concept of error-correlation energy and normalization of signal to ensure high convergence rate, better stability and low steady-state error. Contrary to the conventional LMF, the proposed method has more freedom for large step-sizes. Extensive experiments show significant gain in the performance of the proposed $q$-LMF algorithm in comparison to the contemporary techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge