Ubaid M. Al-Saggaf
Regularized Linear Discriminant Analysis Using a Nonlinear Covariance Matrix Estimator
Feb 07, 2024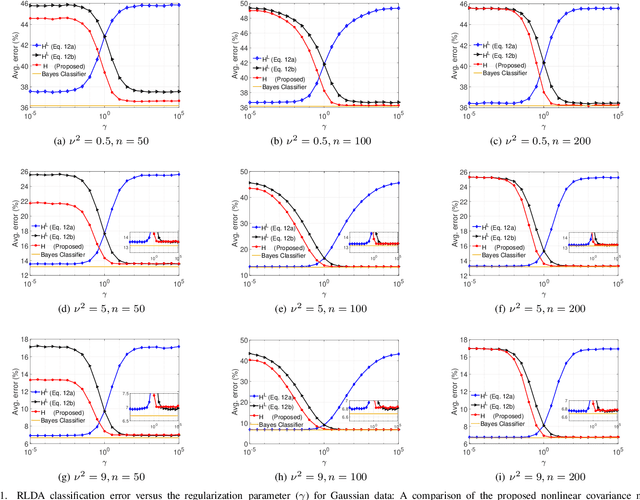
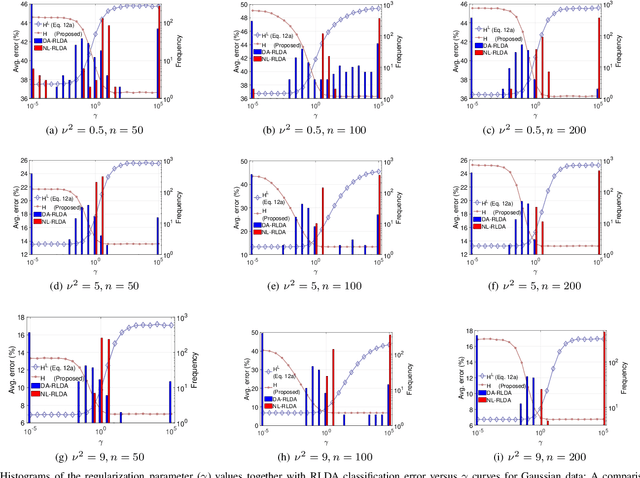
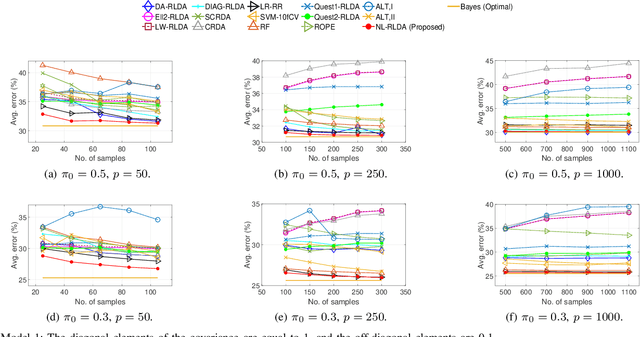
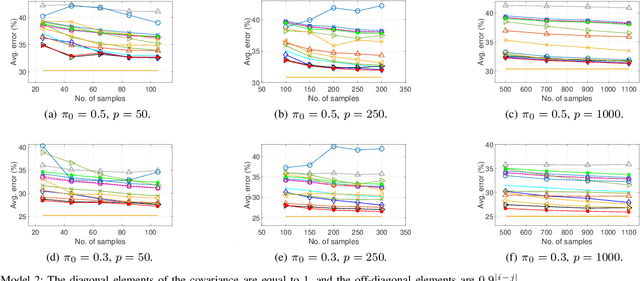
Abstract:Linear discriminant analysis (LDA) is a widely used technique for data classification. The method offers adequate performance in many classification problems, but it becomes inefficient when the data covariance matrix is ill-conditioned. This often occurs when the feature space's dimensionality is higher than or comparable to the training data size. Regularized LDA (RLDA) methods based on regularized linear estimators of the data covariance matrix have been proposed to cope with such a situation. The performance of RLDA methods is well studied, with optimal regularization schemes already proposed. In this paper, we investigate the capability of a positive semidefinite ridge-type estimator of the inverse covariance matrix that coincides with a nonlinear (NL) covariance matrix estimator. The estimator is derived by reformulating the score function of the optimal classifier utilizing linear estimation methods, which eventually results in the proposed NL-RLDA classifier. We derive asymptotic and consistent estimators of the proposed technique's misclassification rate under the assumptions of a double-asymptotic regime and multivariate Gaussian model for the classes. The consistent estimator, coupled with a one-dimensional grid search, is used to set the value of the regularization parameter required for the proposed NL-RLDA classifier. Performance evaluations based on both synthetic and real data demonstrate the effectiveness of the proposed classifier. The proposed technique outperforms state-of-art methods over multiple datasets. When compared to state-of-the-art methods across various datasets, the proposed technique exhibits superior performance.
q-LMF: Quantum Calculus-based Least Mean Fourth Algorithm
Dec 20, 2018
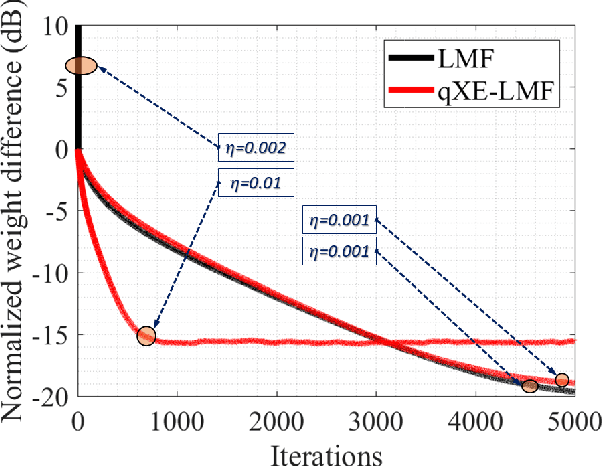
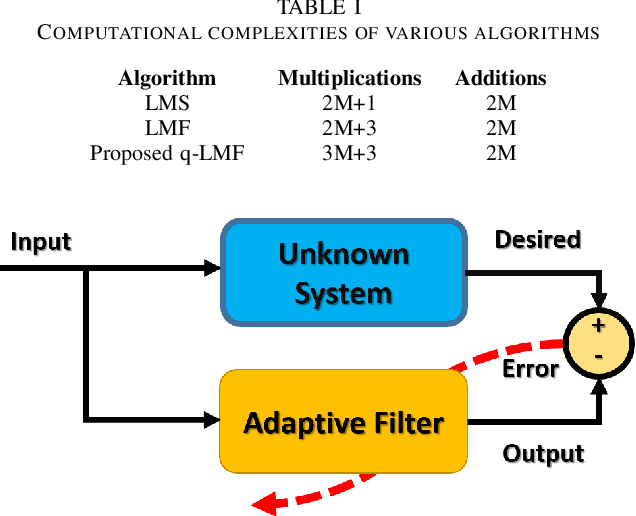
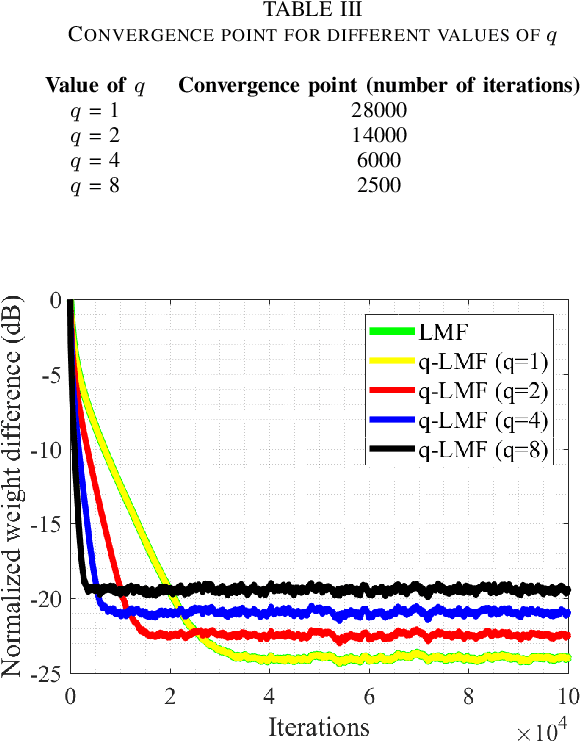
Abstract:Channel estimation is an essential part of modern communication systems as it enhances the overall performance of the system. In recent past a variety of adaptive learning methods have been designed to enhance the robustness and convergence speed of the learning process. However, the need for an optimal technique is still there. Herein, for non-Gaussian noisy environment we propose a new class of stochastic gradient algorithm for channel identification. The proposed $q$-least mean fourth ($q$-LMF) is an extension of least mean fourth (LMF) algorithm and it is based on the $q$-calculus which is also known as Jackson derivative. The proposed algorithm utilizes a novel concept of error-correlation energy and normalization of signal to ensure high convergence rate, better stability and low steady-state error. Contrary to the conventional LMF, the proposed method has more freedom for large step-sizes. Extensive experiments show significant gain in the performance of the proposed $q$-LMF algorithm in comparison to the contemporary techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge