KAAE: Numerical Reasoning for Knowledge Graphs via Knowledge-aware Attributes Learning

Numerical reasoning is pivotal in various artificial intelligence applications, such as natural language processing and recommender systems, where it involves using entities, relations, and attribute values (e.g., weight, length) to infer new factual relations (e.g., the Nile is longer than the Amazon). However, existing approaches encounter two critical challenges in modeling: (1) semantic relevance-the challenge of insufficiently capturing the necessary contextual interactions among entities, relations, and numerical attributes, often resulting in suboptimal inference; and (2) semantic ambiguity-the difficulty in accurately distinguishing ordinal relationships during numerical reasoning, which compromises the generation of high-quality samples and limits the effectiveness of contrastive learning. To address these challenges, we propose the novel Knowledge-Aware Attributes Embedding model (KAAE) for knowledge graph embeddings in numerical reasoning. Specifically, to overcome the challenge of semantic relevance, we introduce a Mixture-of-Experts-Knowledge-Aware (MoEKA) Encoder, designed to integrate the semantics of entities, relations, and numerical attributes into a joint semantic space. To tackle semantic ambiguity, we implement a new ordinal knowledge contrastive learning (OKCL) strategy that generates high-quality ordinal samples from the original data with the aid of ordinal relations, capturing fine-grained semantic nuances essential for accurate numerical reasoning. Experiments on three public benchmark datasets demonstrate the superior performance of KAAE across various attribute value distributions.

CSGNN: Conquering Noisy Node labels via Dynamic Class-wise Selection

Graph Neural Networks (GNNs) have emerged as a powerful tool for representation learning on graphs, but they often suffer from overfitting and label noise issues, especially when the data is scarce or imbalanced. Different from the paradigm of previous methods that rely on single-node confidence, in this paper, we introduce a novel Class-wise Selection for Graph Neural Networks, dubbed CSGNN, which employs a neighbor-aggregated latent space to adaptively select reliable nodes across different classes. Specifically, 1) to tackle the class imbalance issue, we introduce a dynamic class-wise selection mechanism, leveraging the clustering technique to identify clean nodes based on the neighbor-aggregated confidences. In this way, our approach can avoid the pitfalls of biased sampling which is common with global threshold techniques. 2) To alleviate the problem of noisy labels, built on the concept of the memorization effect, CSGNN prioritizes learning from clean nodes before noisy ones, thereby iteratively enhancing model performance while mitigating label noise. Through extensive experiments, we demonstrate that CSGNN outperforms state-of-the-art methods in terms of both effectiveness and robustness.

Geometry Interaction Knowledge Graph Embeddings

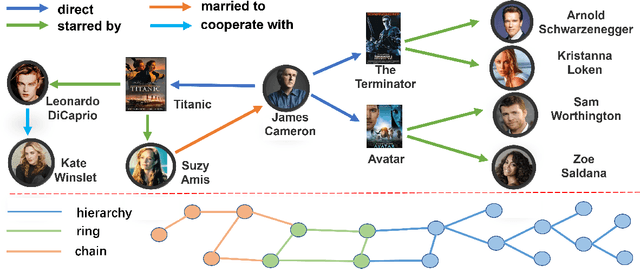
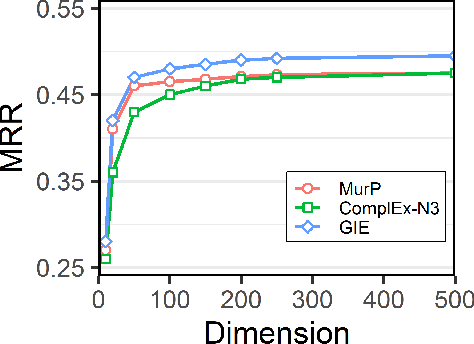
Knowledge graph (KG) embeddings have shown great power in learning representations of entities and relations for link prediction tasks. Previous work usually embeds KGs into a single geometric space such as Euclidean space (zero curved), hyperbolic space (negatively curved) or hyperspherical space (positively curved) to maintain their specific geometric structures (e.g., chain, hierarchy and ring structures). However, the topological structure of KGs appears to be complicated, since it may contain multiple types of geometric structures simultaneously. Therefore, embedding KGs in a single space, no matter the Euclidean space, hyperbolic space or hyperspheric space, cannot capture the complex structures of KGs accurately. To overcome this challenge, we propose Geometry Interaction knowledge graph Embeddings (GIE), which learns spatial structures interactively between the Euclidean, hyperbolic and hyperspherical spaces. Theoretically, our proposed GIE can capture a richer set of relational information, model key inference patterns, and enable expressive semantic matching across entities. Experimental results on three well-established knowledge graph completion benchmarks show that our GIE achieves the state-of-the-art performance with fewer parameters.

ER: Equivariance Regularizer for Knowledge Graph Completion

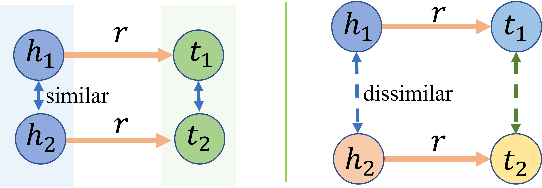
Tensor factorization and distanced based models play important roles in knowledge graph completion (KGC). However, the relational matrices in KGC methods often induce a high model complexity, bearing a high risk of overfitting. As a remedy, researchers propose a variety of different regularizers such as the tensor nuclear norm regularizer. Our motivation is based on the observation that the previous work only focuses on the "size" of the parametric space, while leaving the implicit semantic information widely untouched. To address this issue, we propose a new regularizer, namely, Equivariance Regularizer (ER), which can suppress overfitting by leveraging the implicit semantic information. Specifically, ER can enhance the generalization ability of the model by employing the semantic equivariance between the head and tail entities. Moreover, it is a generic solution for both distance based models and tensor factorization based models. The experimental results indicate a clear and substantial improvement over the state-of-the-art relation prediction methods.