Geometry Interaction Knowledge Graph Embeddings
Paper and Code
Jun 24, 2022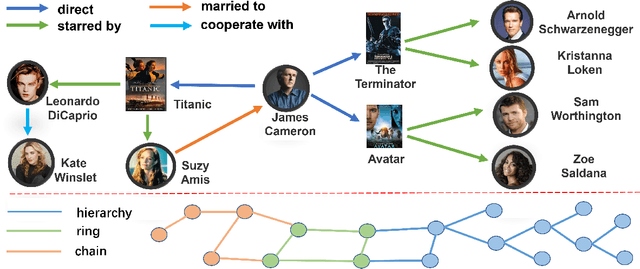


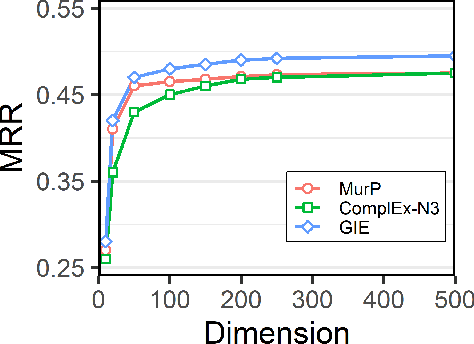
Knowledge graph (KG) embeddings have shown great power in learning representations of entities and relations for link prediction tasks. Previous work usually embeds KGs into a single geometric space such as Euclidean space (zero curved), hyperbolic space (negatively curved) or hyperspherical space (positively curved) to maintain their specific geometric structures (e.g., chain, hierarchy and ring structures). However, the topological structure of KGs appears to be complicated, since it may contain multiple types of geometric structures simultaneously. Therefore, embedding KGs in a single space, no matter the Euclidean space, hyperbolic space or hyperspheric space, cannot capture the complex structures of KGs accurately. To overcome this challenge, we propose Geometry Interaction knowledge graph Embeddings (GIE), which learns spatial structures interactively between the Euclidean, hyperbolic and hyperspherical spaces. Theoretically, our proposed GIE can capture a richer set of relational information, model key inference patterns, and enable expressive semantic matching across entities. Experimental results on three well-established knowledge graph completion benchmarks show that our GIE achieves the state-of-the-art performance with fewer parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge