HotSpot: Screened Poisson Equation for Signed Distance Function Optimization

We propose a method, HotSpot, for optimizing neural signed distance functions, based on a relation between the solution of a screened Poisson equation and the distance function. Existing losses such as the eikonal loss cannot guarantee the recovered implicit function to be a distance function, even when the implicit function satisfies the eikonal equation almost everywhere. Furthermore, the eikonal loss suffers from stability issues in optimization and the remedies that introduce area or divergence minimization can lead to oversmoothing. We address these challenges by designing a loss function that when minimized can converge to the true distance function, is stable, and naturally penalize large surface area. We provide theoretical analysis and experiments on both challenging 2D and 3D datasets and show that our method provide better surface reconstruction and more accurate distance approximation.

OpenIllumination: A Multi-Illumination Dataset for Inverse Rendering Evaluation on Real Objects

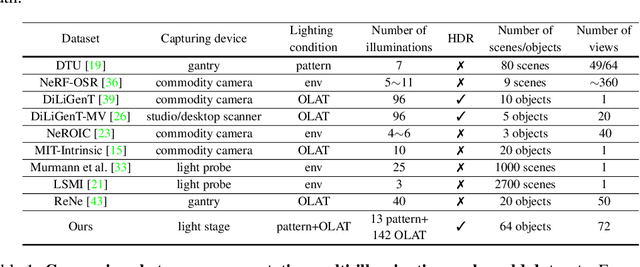
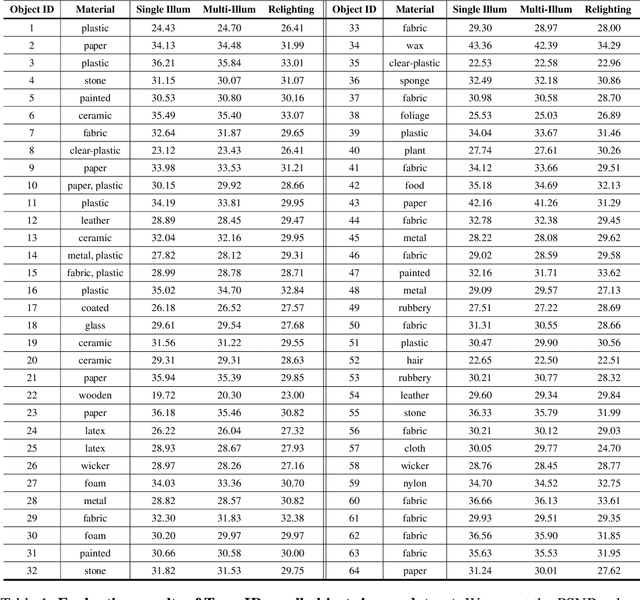
We introduce OpenIllumination, a real-world dataset containing over 108K images of 64 objects with diverse materials, captured under 72 camera views and a large number of different illuminations. For each image in the dataset, we provide accurate camera parameters, illumination ground truth, and foreground segmentation masks. Our dataset enables the quantitative evaluation of most inverse rendering and material decomposition methods for real objects. We examine several state-of-the-art inverse rendering methods on our dataset and compare their performances. The dataset and code can be found on the project page: https://oppo-us-research.github.io/OpenIllumination.