Distance Marching for Generative Modeling

Time-unconditional generative models learn time-independent denoising vector fields. But without time conditioning, the same noisy input may correspond to multiple noise levels and different denoising directions, which interferes with the supervision signal. Inspired by distance field modeling, we propose Distance Marching, a new time-unconditional approach with two principled inference methods. Crucially, we design losses that focus on closer targets. This yields denoising directions better directed toward the data manifold. Across architectures, Distance Marching consistently improves FID by 13.5% on CIFAR-10 and ImageNet over recent time-unconditional baselines. For class-conditional ImageNet generation, despite removing time input, Distance Marching surpasses flow matching using our losses and inference methods. It achieves lower FID than flow matching's final performance using 60% of the sampling steps and 13.6% lower FID on average across backbone sizes. Moreover, our distance prediction is also helpful for early stopping during sampling and for OOD detection. We hope distance field modeling can serve as a principled lens for generative modeling.

HotSpot: Screened Poisson Equation for Signed Distance Function Optimization

We propose a method, HotSpot, for optimizing neural signed distance functions, based on a relation between the solution of a screened Poisson equation and the distance function. Existing losses such as the eikonal loss cannot guarantee the recovered implicit function to be a distance function, even when the implicit function satisfies the eikonal equation almost everywhere. Furthermore, the eikonal loss suffers from stability issues in optimization and the remedies that introduce area or divergence minimization can lead to oversmoothing. We address these challenges by designing a loss function that when minimized can converge to the true distance function, is stable, and naturally penalize large surface area. We provide theoretical analysis and experiments on both challenging 2D and 3D datasets and show that our method provide better surface reconstruction and more accurate distance approximation.

House Price Valuation Model Based on Geographically Neural Network Weighted Regression: The Case Study of Shenzhen, China

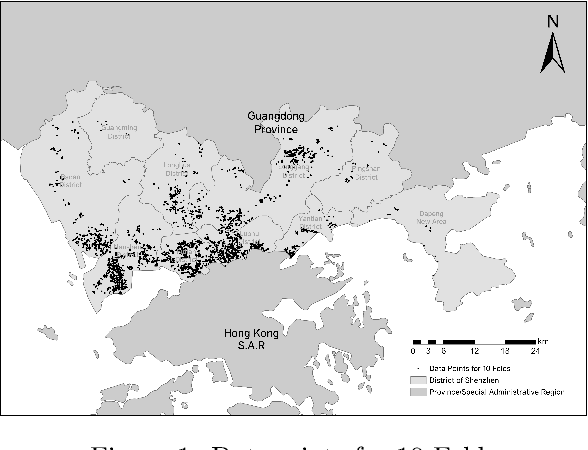
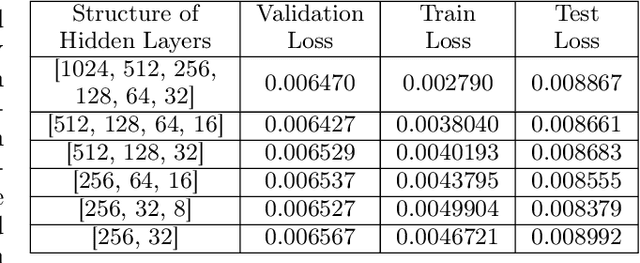
Confronted with the spatial heterogeneity of real estate market, some traditional research utilized Geographically Weighted Regression (GWR) to estimate the house price. However, its kernel function is non-linear, elusive, and complex to opt bandwidth, the predictive power could also be improved. Consequently, a novel technique, Geographical Neural Network Weighted Regression (GNNWR), has been applied to improve the accuracy of real estate appraisal with the help of neural networks. Based on Shenzhen house price dataset, this work conspicuously captures the weight distribution of different variants at Shenzhen real estate market, which GWR is difficult to materialize. Moreover, we focus on the performance of GNNWR, verify its robustness and superiority, refine the experiment process with 10-fold cross-validation, extend its application area from natural to socioeconomic geospatial data. It's a practical and trenchant way to assess house price, and we demonstrate the effectiveness of GNNWR on a complex socioeconomic dataset.