GeoUni: A Unified Model for Generating Geometry Diagrams, Problems and Problem Solutions

We propose GeoUni, the first unified geometry expert model capable of generating problem solutions and diagrams within a single framework in a way that enables the creation of unique and individualized geometry problems. Traditionally, solving geometry problems and generating diagrams have been treated as separate tasks in machine learning, with no models successfully integrating both to support problem creation. However, we believe that mastery in geometry requires frictionless integration of all of these skills, from solving problems to visualizing geometric relationships, and finally, crafting tailored problems. Our extensive experiments demonstrate that GeoUni, with only 1.5B parameters, achieves performance comparable to larger models such as DeepSeek-R1 with 671B parameters in geometric reasoning tasks. GeoUni also excels in generating precise geometric diagrams, surpassing both text-to-image models and unified models, including the GPT-4o image generation. Most importantly, GeoUni is the only model capable of successfully generating textual problems with matching diagrams based on specific knowledge points, thus offering a wider range of capabilities that extend beyond current models.

Head-Aware KV Cache Compression for Efficient Visual Autoregressive Modeling

Visual Autoregressive (VAR) models have emerged as a powerful approach for multi-modal content creation, offering high efficiency and quality across diverse multimedia applications. However, they face significant memory bottlenecks due to extensive KV cache accumulation during inference. Existing KV cache compression techniques for large language models are suboptimal for VAR models due to, as we identify in this paper, two distinct categories of attention heads in VAR models: Structural Heads, which preserve spatial coherence through diagonal attention patterns, and Contextual Heads, which maintain semantic consistency through vertical attention patterns. These differences render single-strategy KV compression techniques ineffective for VAR models. To address this, we propose HACK, a training-free Head-Aware Compression method for KV cache. HACK allocates asymmetric cache budgets and employs pattern-specific compression strategies tailored to the essential characteristics of each head category. Experiments on Infinity-2B, Infinity-8B, and VAR-d30 demonstrate its effectiveness in text-to-image and class-conditional generation tasks. HACK can hack down up to 50\% and 70\% of cache with minimal performance degradation for VAR-d30 and Infinity-8B, respectively. Even with 70\% and 90\% KV cache compression in VAR-d30 and Infinity-8B, HACK still maintains high-quality generation while reducing memory usage by 44.2\% and 58.9\%, respectively.

CAKE: Cascading and Adaptive KV Cache Eviction with Layer Preferences

Large language models (LLMs) excel at processing long sequences, boosting demand for key-value (KV) caching. While recent efforts to evict KV cache have alleviated the inference burden, they often fail to allocate resources rationally across layers with different attention patterns. In this paper, we introduce Cascading and Adaptive KV cache Eviction (CAKE), a novel approach that frames KV cache eviction as a "cake-slicing problem." CAKE assesses layer-specific preferences by considering attention dynamics in both spatial and temporal dimensions, allocates rational cache size for layers accordingly, and manages memory constraints in a cascading manner. This approach enables a global view of cache allocation, adaptively distributing resources across diverse attention mechanisms while maintaining memory budgets. CAKE also employs a new eviction indicator that considers the shifting importance of tokens over time, addressing limitations in existing methods that overlook temporal dynamics. Comprehensive experiments on LongBench and NeedleBench show that CAKE maintains model performance with only 3.2% of the KV cache and consistently outperforms current baselines across various models and memory constraints, particularly in low-memory settings. Additionally, CAKE achieves over 10x speedup in decoding latency compared to full cache when processing contexts of 128K tokens with FlashAttention-2. Our code is available at https://github.com/antgroup/cakekv.

Diagram Formalization Enhanced Multi-Modal Geometry Problem Solver

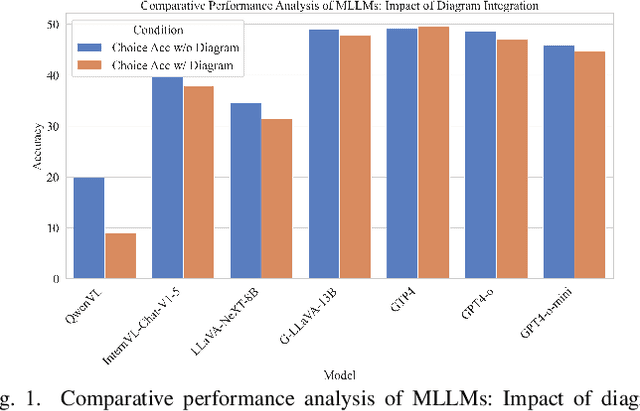
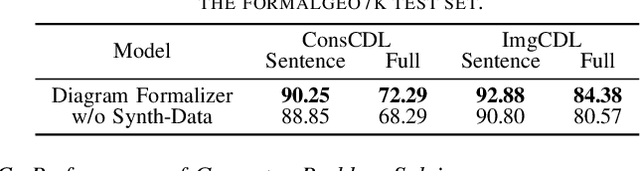
Mathematical reasoning remains an ongoing challenge for AI models, especially for geometry problems that require both linguistic and visual signals. As the vision encoders of most MLLMs are trained on natural scenes, they often struggle to understand geometric diagrams, performing no better in geometry problem solving than LLMs that only process text. This limitation is amplified by the lack of effective methods for representing geometric relationships. To address these issues, we introduce the Diagram Formalization Enhanced Geometry Problem Solver (DFE-GPS), a new framework that integrates visual features, geometric formal language, and natural language representations. We propose a novel synthetic data approach and create a large-scale geometric dataset, SynthGeo228K, annotated with both formal and natural language captions, designed to enhance the vision encoder for a better understanding of geometric structures. Our framework improves MLLMs' ability to process geometric diagrams and extends their application to open-ended tasks on the formalgeo7k dataset.

Low-Rank Winograd Transformation for 3D Convolutional Neural Networks

This paper focuses on Winograd transformation in 3D convolutional neural networks (CNNs) that are more over-parameterized compared with the 2D version. The over-increasing Winograd parameters not only exacerbate training complexity but also barricade the practical speedups due simply to the volume of element-wise products in the Winograd domain. We attempt to reduce trainable parameters by introducing a low-rank Winograd transformation, a novel training paradigm that decouples the original large tensor into two less storage-required trainable tensors, leading to a significant complexity reduction. Built upon our low-rank Winograd transformation, we take one step ahead by proposing a low-rank oriented sparse granularity that measures column-wise parameter importance. By simply involving the non-zero columns in the element-wise product, our sparse granularity is empowered with the ability to produce a very regular sparse pattern to acquire effectual Winograd speedups. To better understand the efficacy of our method, we perform extensive experiments on 3D CNNs. Results manifest that our low-rank Winograd transformation well outperforms the vanilla Winograd transformation. We also show that our proposed low-rank oriented sparse granularity permits practical Winograd acceleration compared with the vanilla counterpart.