Diagram Formalization Enhanced Multi-Modal Geometry Problem Solver

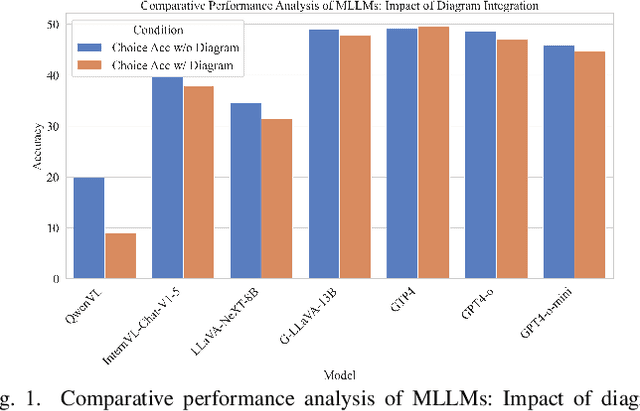
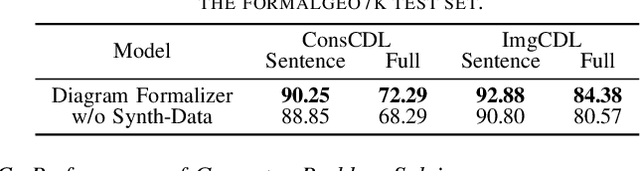
Mathematical reasoning remains an ongoing challenge for AI models, especially for geometry problems that require both linguistic and visual signals. As the vision encoders of most MLLMs are trained on natural scenes, they often struggle to understand geometric diagrams, performing no better in geometry problem solving than LLMs that only process text. This limitation is amplified by the lack of effective methods for representing geometric relationships. To address these issues, we introduce the Diagram Formalization Enhanced Geometry Problem Solver (DFE-GPS), a new framework that integrates visual features, geometric formal language, and natural language representations. We propose a novel synthetic data approach and create a large-scale geometric dataset, SynthGeo228K, annotated with both formal and natural language captions, designed to enhance the vision encoder for a better understanding of geometric structures. Our framework improves MLLMs' ability to process geometric diagrams and extends their application to open-ended tasks on the formalgeo7k dataset.

FGeo-HyperGNet: Geometry Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network

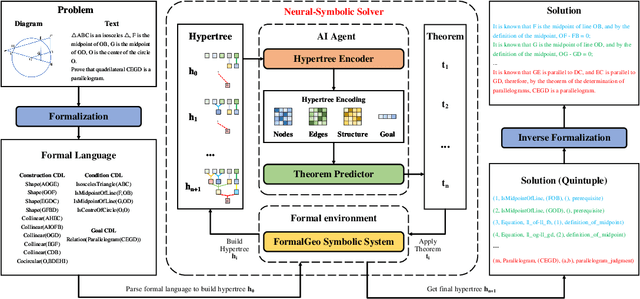
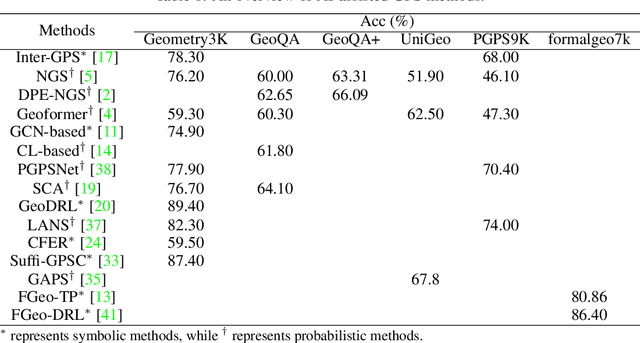
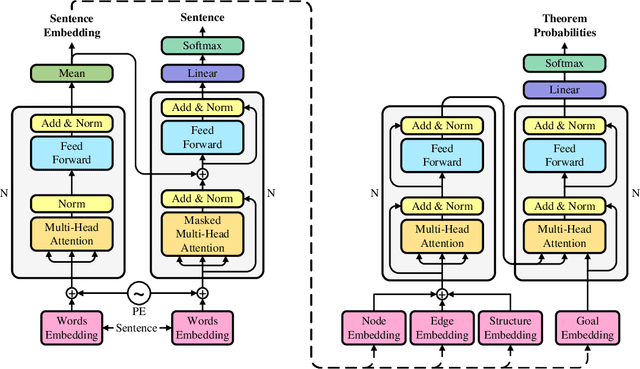
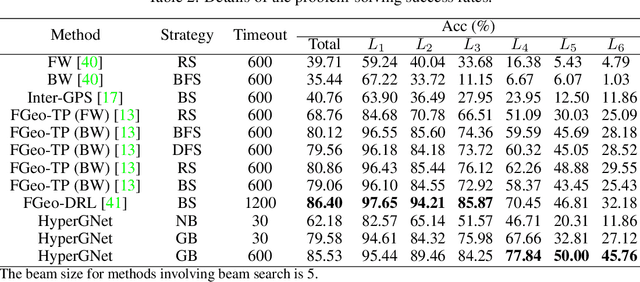
Geometry problem solving has always been a long-standing challenge in the fields of automated reasoning and artificial intelligence. This is the fifth article in a series of our works, we built a neural-symbolic system to automatically perform human-like geometric deductive reasoning. The symbolic part is a formal system built on FormalGeo, which can automatically perform geomertic relational reasoning and algebraic calculations and organize the solving process into a solution hypertree with conditions as hypernodes and theorems as hyperedges. The neural part, called HyperGNet, is a hypergraph neural network based on the attention mechanism, including a encoder to effectively encode the structural and semantic information of the hypertree, and a solver to provide problem-solving guidance. The neural part predicts theorems according to the hypertree, and the symbolic part applies theorems and updates the hypertree, thus forming a Predict-Apply Cycle to ultimately achieve readable and traceable automatic solving of geometric problems. Experiments demonstrate the correctness and effectiveness of this neural-symbolic architecture. We achieved a step-wised accuracy of 87.65% and an overall accuracy of 85.53% on the formalgeo7k datasets. The code and data is available at https://github.com/BitSecret/HyperGNet.

FGeo-DRL: Deductive Reasoning for Geometric Problems through Deep Reinforcement Learning

The human-like automatic deductive reasoning has always been one of the most challenging open problems in the interdiscipline of mathematics and artificial intelligence. This paper is the third in a series of our works. We built a neural-symbolic system, called FGeoDRL, to automatically perform human-like geometric deductive reasoning. The neural part is an AI agent based on reinforcement learning, capable of autonomously learning problem-solving methods from the feedback of a formalized environment, without the need for human supervision. It leverages a pre-trained natural language model to establish a policy network for theorem selection and employ Monte Carlo Tree Search for heuristic exploration. The symbolic part is a reinforcement learning environment based on geometry formalization theory and FormalGeo, which models GPS as a Markov Decision Process. In this formal symbolic system, the known conditions and objectives of the problem form the state space, while the set of theorems forms the action space. Leveraging FGeoDRL, we have achieved readable and verifiable automated solutions to geometric problems. Experiments conducted on the formalgeo7k dataset have achieved a problem-solving success rate of 86.40%. The project is available at https://github.com/PersonNoName/FGeoDRL.

FGeo-TP: A Language Model-Enhanced Solver for Geometry Problems

The application of contemporary artificial intelligence techniques to address geometric problems and automated deductive proof has always been a grand challenge to the interdiscipline field of mathematics and artificial Intelligence. This is the fourth article in a series of our works, in our previous work, we established of a geometric formalized system known as FormalGeo. Moreover we annotated approximately 7000 geometric problems, forming the FormalGeo7k dataset. Despite the FGPS (Formal Geometry Problem Solver) can achieve interpretable algebraic equation solving and human-like deductive reasoning, it often experiences timeouts due to the complexity of the search strategy. In this paper, we introduced FGeo-TP (Theorem Predictor), which utilizes the language model to predict theorem sequences for solving geometry problems. We compared the effectiveness of various Transformer architectures, such as BART or T5, in theorem prediction, implementing pruning in the search process of FGPS, thereby improving its performance in solving geometry problems. Our results demonstrate a significant increase in the problem-solving rate of the language model-enhanced FGeo-TP on the FormalGeo7k dataset, rising from 39.7% to 80.86%. Furthermore, FGeo-TP exhibits notable reductions in solving time and search steps across problems of varying difficulty levels.

FormalGeo: The First Step Toward Human-like IMO-level Geometric Automated Reasoning

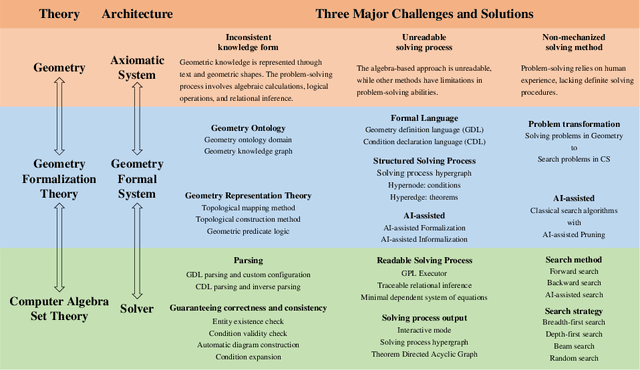
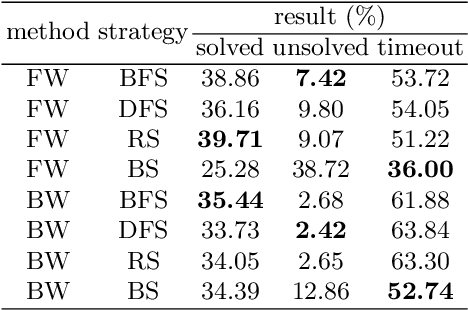
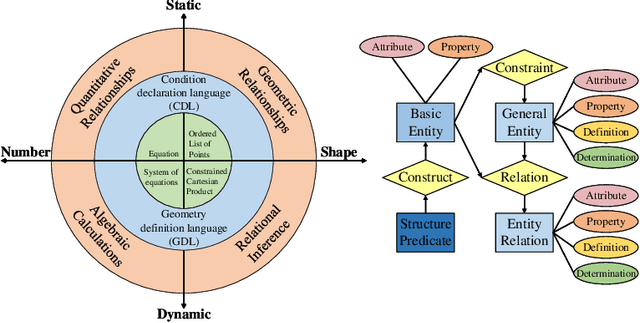
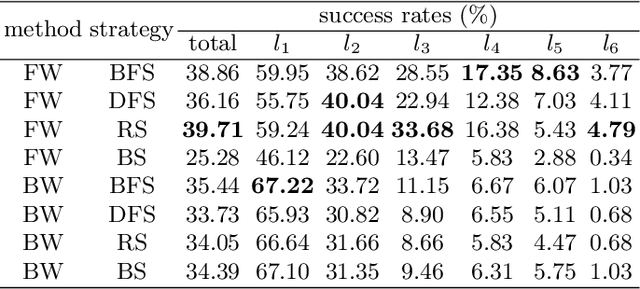
This is the first paper in a series of work we have accomplished over the past three years. In this paper, we have constructed a complete and compatible formal plane geometry system. This will serve as a crucial bridge between IMO-level plane geometry challenges and readable AI automated reasoning. With this formal system in place, we have been able to seamlessly integrate modern AI models with our formal system. Within this formal framework, AI is now capable of providing deductive reasoning solutions to IMO-level plane geometry problems, just like handling other natural languages, and these proofs are readable, traceable, and verifiable. We propose the geometry formalization theory (GFT) to guide the development of the geometry formal system. Based on the GFT, we have established the FormalGeo, which consists of 88 geometric predicates and 196 theorems. It can represent, validate, and solve IMO-level geometry problems. we also have crafted the FGPS (formal geometry problem solver) in Python. It serves as both an interactive assistant for verifying problem-solving processes and an automated problem solver, utilizing various methods such as forward search, backward search and AI-assisted search. We've annotated the FormalGeo7k dataset, containing 6,981 (expand to 186,832 through data augmentation) geometry problems with complete formal language annotations. Implementation of the formal system and experiments on the FormalGeo7k validate the correctness and utility of the GFT. The backward depth-first search method only yields a 2.42% problem-solving failure rate, and we can incorporate deep learning techniques to achieve lower one. The source code of FGPS and FormalGeo7k dataset are available at https://github.com/BitSecret/FormalGeo.

Towards Better Orthogonality Regularization with Disentangled Norm in Training Deep CNNs

Orthogonality regularization has been developed to prevent deep CNNs from training instability and feature redundancy. Among existing proposals, kernel orthogonality regularization enforces orthogonality by minimizing the residual between the Gram matrix formed by convolutional filters and the orthogonality matrix. We propose a novel measure for achieving better orthogonality among filters, which disentangles diagonal and correlation information from the residual. The model equipped with the measure under the principle of imposing strict orthogonality between filters surpasses previous regularization methods in near-orthogonality. Moreover, we observe the benefits of improved strict filter orthogonality in relatively shallow models, but as model depth increases, the performance gains in models employing strict kernel orthogonality decrease sharply. Furthermore, based on the observation of the potential conflict between strict kernel orthogonality and growing model capacity, we propose a relaxation theory on kernel orthogonality regularization. The relaxed kernel orthogonality achieves enhanced performance on models with increased capacity, shedding light on the burden of strict kernel orthogonality on deep model performance. We conduct extensive experiments with our kernel orthogonality regularization toolkit on ResNet and WideResNet in CIFAR-10 and CIFAR-100. We observe state-of-the-art gains in model performance from the toolkit, which includes both strict orthogonality and relaxed orthogonality regularization, and obtain more robust models with expressive features. These experiments demonstrate the efficacy of our toolkit and subtly provide insights into the often overlooked challenges posed by strict orthogonality, addressing the burden of strict orthogonality on capacity-rich models.

Variational AutoEncoder For Regression: Application to Brain Aging Analysis

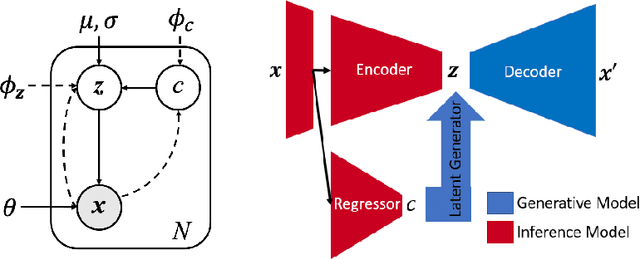
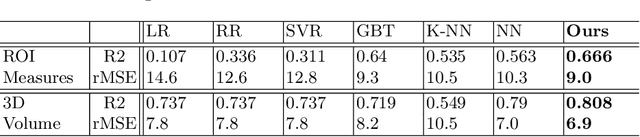
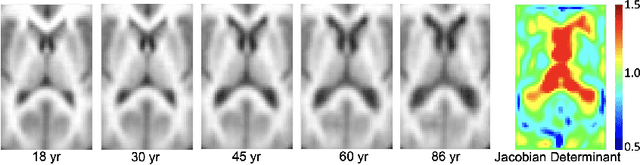
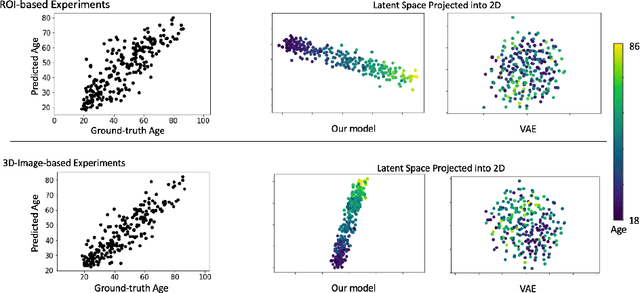
While unsupervised variational autoencoders (VAE) have become a powerful tool in neuroimage analysis, their application to supervised learning is under-explored. We aim to close this gap by proposing a unified probabilistic model for learning the latent space of imaging data and performing supervised regression. Based on recent advances in learning disentangled representations, the novel generative process explicitly models the conditional distribution of latent representations with respect to the regression target variable. Performing a variational inference procedure on this model leads to joint regularization between the VAE and a neural-network regressor. In predicting the age of 245 subjects from their structural Magnetic Resonance (MR) images, our model is more accurate than state-of-the-art methods when applied to either region-of-interest (ROI) measurements or raw 3D volume images. More importantly, unlike simple feed-forward neural-networks, disentanglement of age in latent representations allows for intuitive interpretation of the structural developmental patterns of the human brain.