FGeo-HyperGNet: Geometry Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network

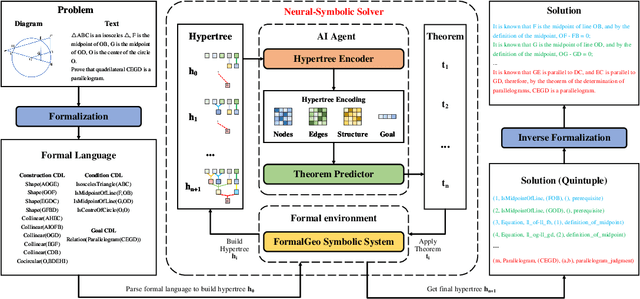
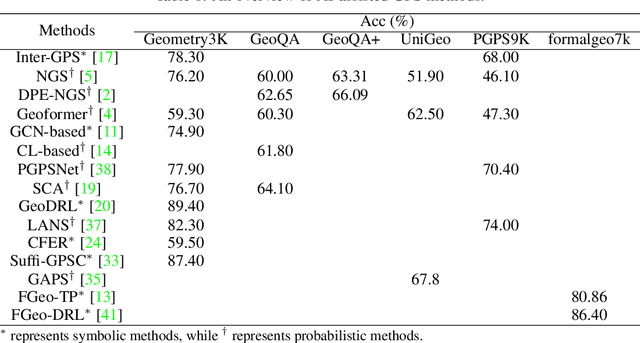
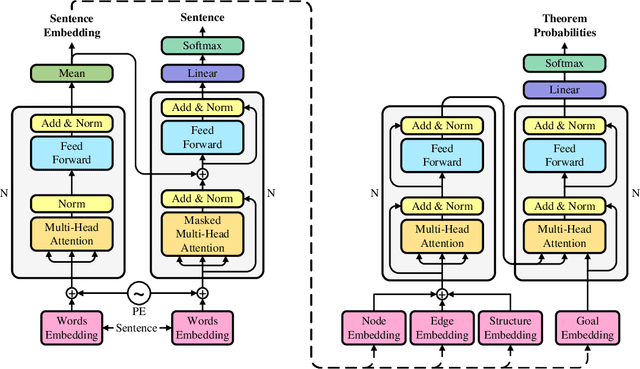
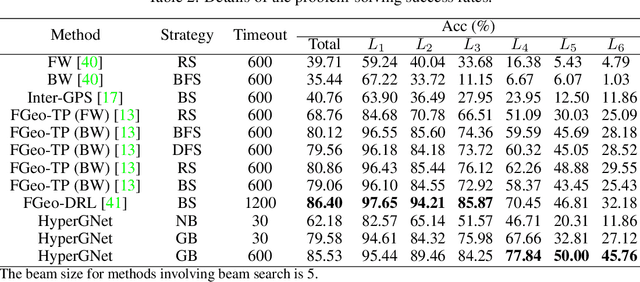
Geometry problem solving has always been a long-standing challenge in the fields of automated reasoning and artificial intelligence. This is the fifth article in a series of our works, we built a neural-symbolic system to automatically perform human-like geometric deductive reasoning. The symbolic part is a formal system built on FormalGeo, which can automatically perform geomertic relational reasoning and algebraic calculations and organize the solving process into a solution hypertree with conditions as hypernodes and theorems as hyperedges. The neural part, called HyperGNet, is a hypergraph neural network based on the attention mechanism, including a encoder to effectively encode the structural and semantic information of the hypertree, and a solver to provide problem-solving guidance. The neural part predicts theorems according to the hypertree, and the symbolic part applies theorems and updates the hypertree, thus forming a Predict-Apply Cycle to ultimately achieve readable and traceable automatic solving of geometric problems. Experiments demonstrate the correctness and effectiveness of this neural-symbolic architecture. We achieved a step-wised accuracy of 87.65% and an overall accuracy of 85.53% on the formalgeo7k datasets. The code and data is available at https://github.com/BitSecret/HyperGNet.