FGeo-HyperGNet: Geometry Problem Solving Integrating Formal Symbolic System and Hypergraph Neural Network

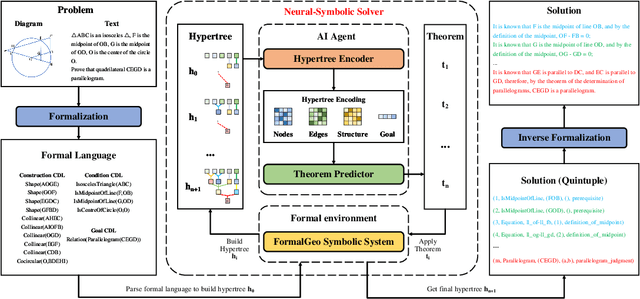
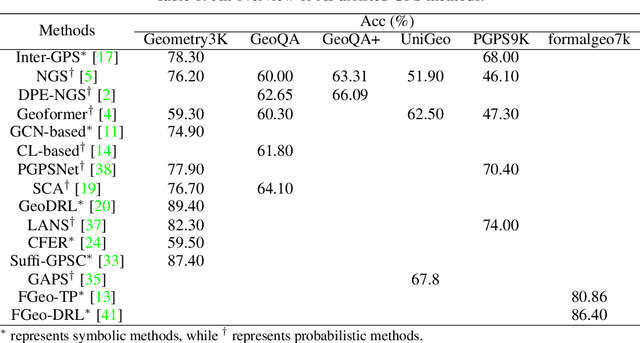
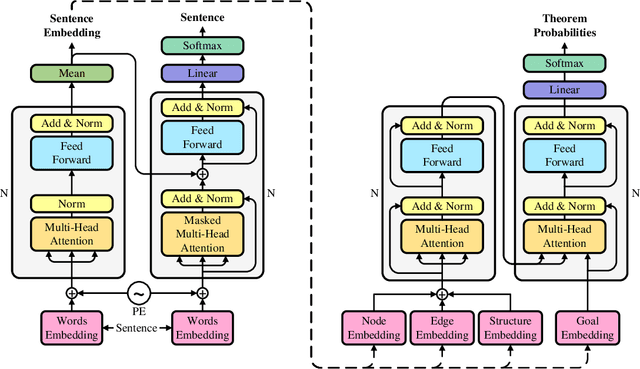
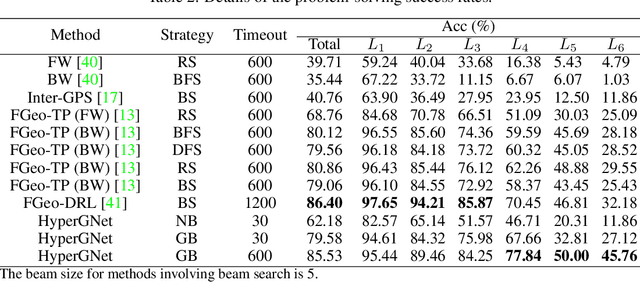
Geometry problem solving has always been a long-standing challenge in the fields of automated reasoning and artificial intelligence. This is the fifth article in a series of our works, we built a neural-symbolic system to automatically perform human-like geometric deductive reasoning. The symbolic part is a formal system built on FormalGeo, which can automatically perform geomertic relational reasoning and algebraic calculations and organize the solving process into a solution hypertree with conditions as hypernodes and theorems as hyperedges. The neural part, called HyperGNet, is a hypergraph neural network based on the attention mechanism, including a encoder to effectively encode the structural and semantic information of the hypertree, and a solver to provide problem-solving guidance. The neural part predicts theorems according to the hypertree, and the symbolic part applies theorems and updates the hypertree, thus forming a Predict-Apply Cycle to ultimately achieve readable and traceable automatic solving of geometric problems. Experiments demonstrate the correctness and effectiveness of this neural-symbolic architecture. We achieved a step-wised accuracy of 87.65% and an overall accuracy of 85.53% on the formalgeo7k datasets. The code and data is available at https://github.com/BitSecret/HyperGNet.

FormalGeo: The First Step Toward Human-like IMO-level Geometric Automated Reasoning

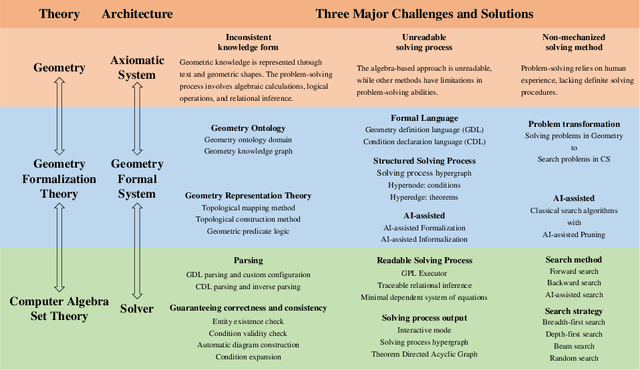
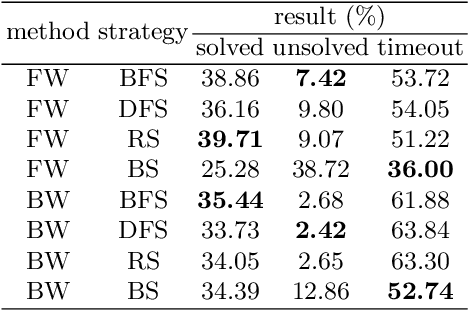
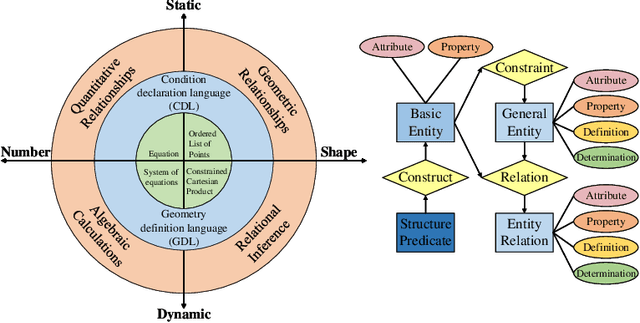
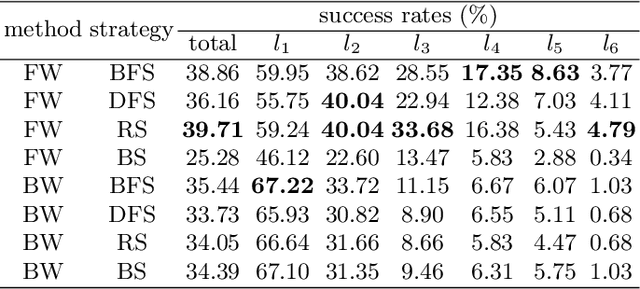
This is the first paper in a series of work we have accomplished over the past three years. In this paper, we have constructed a complete and compatible formal plane geometry system. This will serve as a crucial bridge between IMO-level plane geometry challenges and readable AI automated reasoning. With this formal system in place, we have been able to seamlessly integrate modern AI models with our formal system. Within this formal framework, AI is now capable of providing deductive reasoning solutions to IMO-level plane geometry problems, just like handling other natural languages, and these proofs are readable, traceable, and verifiable. We propose the geometry formalization theory (GFT) to guide the development of the geometry formal system. Based on the GFT, we have established the FormalGeo, which consists of 88 geometric predicates and 196 theorems. It can represent, validate, and solve IMO-level geometry problems. we also have crafted the FGPS (formal geometry problem solver) in Python. It serves as both an interactive assistant for verifying problem-solving processes and an automated problem solver, utilizing various methods such as forward search, backward search and AI-assisted search. We've annotated the FormalGeo7k dataset, containing 6,981 (expand to 186,832 through data augmentation) geometry problems with complete formal language annotations. Implementation of the formal system and experiments on the FormalGeo7k validate the correctness and utility of the GFT. The backward depth-first search method only yields a 2.42% problem-solving failure rate, and we can incorporate deep learning techniques to achieve lower one. The source code of FGPS and FormalGeo7k dataset are available at https://github.com/BitSecret/FormalGeo.

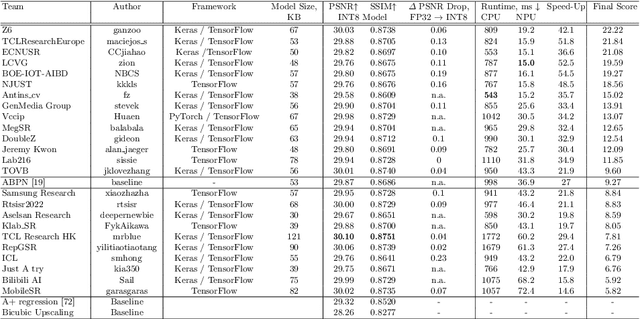
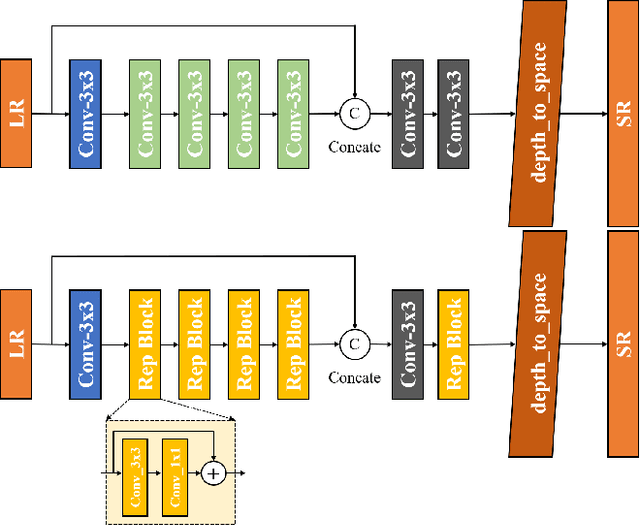
Efficient and Accurate Quantized Image Super-Resolution on Mobile NPUs, Mobile AI & AIM 2022 challenge: Report

Image super-resolution is a common task on mobile and IoT devices, where one often needs to upscale and enhance low-resolution images and video frames. While numerous solutions have been proposed for this problem in the past, they are usually not compatible with low-power mobile NPUs having many computational and memory constraints. In this Mobile AI challenge, we address this problem and propose the participants to design an efficient quantized image super-resolution solution that can demonstrate a real-time performance on mobile NPUs. The participants were provided with the DIV2K dataset and trained INT8 models to do a high-quality 3X image upscaling. The runtime of all models was evaluated on the Synaptics VS680 Smart Home board with a dedicated edge NPU capable of accelerating quantized neural networks. All proposed solutions are fully compatible with the above NPU, demonstrating an up to 60 FPS rate when reconstructing Full HD resolution images. A detailed description of all models developed in the challenge is provided in this paper.