Learning Mixtures of Plackett-Luce Models with Features from Top-$l$ Orders

Plackett-Luce model (PL) is one of the most popular models for preference learning. In this paper, we consider PL with features and its mixture models, where each alternative has a vector of features, possibly different across agents. Such models significantly generalize the standard PL, but are not as well investigated in the literature. We extend mixtures of PLs with features to models that generate top-$l$ and characterize their identifiability. We further prove that when PL with features is identifiable, its MLE is consistent with a strictly concave objective function under mild assumptions. Our experiments on synthetic data demonstrate the effectiveness of MLE on PL with features with tradeoffs between statistical efficiency and computational efficiency when $l$ takes different values. For mixtures of PL with features, we show that an EM algorithm outperforms MLE in MSE and runtime.

Dual Learning: Theoretical Study and an Algorithmic Extension

Dual learning has been successfully applied in many machine learning applications including machine translation, image-to-image transformation, etc. The high-level idea of dual learning is very intuitive: if we map an $x$ from one domain to another and then map it back, we should recover the original $x$. Although its effectiveness has been empirically verified, theoretical understanding of dual learning is still very limited. In this paper, we aim at understanding why and when dual learning works. Based on our theoretical analysis, we further extend dual learning by introducing more related mappings and propose multi-step dual learning, in which we leverage feedback signals from additional domains to improve the qualities of the mappings. We prove that multi-step dual learn-ing can boost the performance of standard dual learning under mild conditions. Experiments on WMT 14 English$\leftrightarrow$German and MultiUNEnglish$\leftrightarrow$French translations verify our theoretical findings on dual learning, and the results on the translations among English, French, and Spanish of MultiUN demonstrate the effectiveness of multi-step dual learning.

Learning Mixtures of Plackett-Luce Models from Structured Partial Orders

Mixtures of ranking models have been widely used for heterogeneous preferences. However, learning a mixture model is highly nontrivial, especially when the dataset consists of partial orders. In such cases, the parameter of the model may not be even identifiable. In this paper, we focus on three popular structures of partial orders: ranked top-$l_1$, $l_2$-way, and choice data over a subset of alternatives. We prove that when the dataset consists of combinations of ranked top-$l_1$ and $l_2$-way (or choice data over up to $l_2$ alternatives), mixture of $k$ Plackett-Luce models is not identifiable when $l_1+l_2\le 2k-1$ ($l_2$ is set to $1$ when there are no $l_2$-way orders). We also prove that under some combinations, including ranked top-$3$, ranked top-$2$ plus $2$-way, and choice data over up to $4$ alternatives, mixtures of two Plackett-Luce models are identifiable. Guided by our theoretical results, we propose efficient generalized method of moments (GMM) algorithms to learn mixtures of two Plackett-Luce models, which are proven consistent. Our experiments demonstrate the efficacy of our algorithms. Moreover, we show that when full rankings are available, learning from different marginal events (partial orders) provides tradeoffs between statistical efficiency and computational efficiency.

Practical Algorithms for Multi-Stage Voting Rules with Parallel Universes Tiebreaking

STV and ranked pairs (RP) are two well-studied voting rules for group decision-making. They proceed in multiple rounds, and are affected by how ties are broken in each round. However, the literature is surprisingly vague about how ties should be broken. We propose the first algorithms for computing the set of alternatives that are winners under some tiebreaking mechanism under STV and RP, which is also known as parallel-universes tiebreaking (PUT). Unfortunately, PUT-winners are NP-complete to compute under STV and RP, and standard search algorithms from AI do not apply. We propose multiple DFS-based algorithms along with pruning strategies, heuristics, sampling and machine learning to prioritize search direction to significantly improve the performance. We also propose novel ILP formulations for PUT-winners under STV and RP, respectively. Experiments on synthetic and real-world data show that our algorithms are overall faster than ILP.

A Cost-Effective Framework for Preference Elicitation and Aggregation

We propose a cost-effective framework for preference elicitation and aggregation under the Plackett-Luce model with features. Given a budget, our framework iteratively computes the most cost-effective elicitation questions in order to help the agents make a better group decision. We illustrate the viability of the framework with experiments on Amazon Mechanical Turk, which we use to estimate the cost of answering different types of elicitation questions. We compare the prediction accuracy of our framework when adopting various information criteria that evaluate the expected information gain from a question. Our experiments show carefully designed information criteria are much more efficient, i.e., they arrive at the correct answer using fewer queries, than randomly asking questions given the budget constraint.

Composite Marginal Likelihood Methods for Random Utility Models

We propose a novel and flexible rank-breaking-then-composite-marginal-likelihood (RBCML) framework for learning random utility models (RUMs), which include the Plackett-Luce model. We characterize conditions for the objective function of RBCML to be strictly log-concave by proving that strict log-concavity is preserved under convolution and marginalization. We characterize necessary and sufficient conditions for RBCML to satisfy consistency and asymptotic normality. Experiments on synthetic data show that RBCML for Gaussian RUMs achieves better statistical efficiency and computational efficiency than the state-of-the-art algorithm and our RBCML for the Plackett-Luce model provides flexible tradeoffs between running time and statistical efficiency.

Practical Algorithms for STV and Ranked Pairs with Parallel Universes Tiebreaking

STV and ranked pairs (RP) are two well-studied voting rules for group decision-making. They proceed in multiple rounds, and are affected by how ties are broken in each round. However, the literature is surprisingly vague about how ties should be broken. We propose the first algorithms for computing the set of alternatives that are winners under some tiebreaking mechanism under STV and RP, which is also known as parallel-universes tiebreaking (PUT). Unfortunately, PUT-winners are NP-complete to compute under STV and RP, and standard search algorithms from AI do not apply. We propose multiple DFS-based algorithms along with pruning strategies and heuristics to prioritize search direction to significantly improve the performance using machine learning. We also propose novel ILP formulations for PUT-winners under STV and RP, respectively. Experiments on synthetic and real-world data show that our algorithms are overall significantly faster than ILP, while there are a few cases where ILP is significantly faster for RP.

Learning Mixtures of Plackett-Luce Models

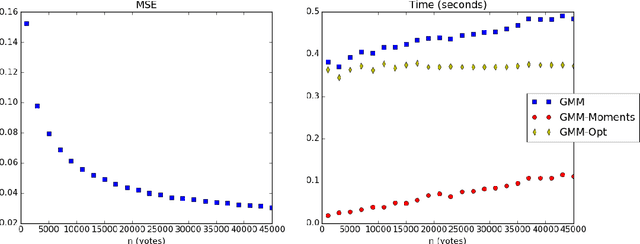
In this paper we address the identifiability and efficient learning problems of finite mixtures of Plackett-Luce models for rank data. We prove that for any $k\geq 2$, the mixture of $k$ Plackett-Luce models for no more than $2k-1$ alternatives is non-identifiable and this bound is tight for $k=2$. For generic identifiability, we prove that the mixture of $k$ Plackett-Luce models over $m$ alternatives is generically identifiable if $k\leq\lfloor\frac {m-2} 2\rfloor!$. We also propose an efficient generalized method of moments (GMM) algorithm to learn the mixture of two Plackett-Luce models and show that the algorithm is consistent. Our experiments show that our GMM algorithm is significantly faster than the EMM algorithm by Gormley and Murphy (2008), while achieving competitive statistical efficiency.