Peter Piech
Learning Mixtures of Plackett-Luce Models
Jun 07, 2016
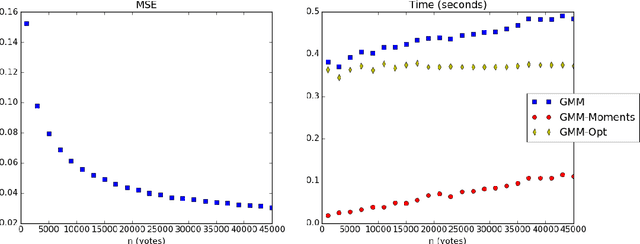
Abstract:In this paper we address the identifiability and efficient learning problems of finite mixtures of Plackett-Luce models for rank data. We prove that for any $k\geq 2$, the mixture of $k$ Plackett-Luce models for no more than $2k-1$ alternatives is non-identifiable and this bound is tight for $k=2$. For generic identifiability, we prove that the mixture of $k$ Plackett-Luce models over $m$ alternatives is generically identifiable if $k\leq\lfloor\frac {m-2} 2\rfloor!$. We also propose an efficient generalized method of moments (GMM) algorithm to learn the mixture of two Plackett-Luce models and show that the algorithm is consistent. Our experiments show that our GMM algorithm is significantly faster than the EMM algorithm by Gormley and Murphy (2008), while achieving competitive statistical efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge