Oscillation Inversion: Understand the structure of Large Flow Model through the Lens of Inversion Method

We explore the oscillatory behavior observed in inversion methods applied to large-scale text-to-image diffusion models, with a focus on the "Flux" model. By employing a fixed-point-inspired iterative approach to invert real-world images, we observe that the solution does not achieve convergence, instead oscillating between distinct clusters. Through both toy experiments and real-world diffusion models, we demonstrate that these oscillating clusters exhibit notable semantic coherence. We offer theoretical insights, showing that this behavior arises from oscillatory dynamics in rectified flow models. Building on this understanding, we introduce a simple and fast distribution transfer technique that facilitates image enhancement, stroke-based recoloring, as well as visual prompt-guided image editing. Furthermore, we provide quantitative results demonstrating the effectiveness of our method for tasks such as image enhancement, makeup transfer, reconstruction quality, and guided sampling quality. Higher-quality examples of videos and images are available at \href{https://yanyanzheng96.github.io/oscillation_inversion/}{this link}.

PPLNs: Parametric Piecewise Linear Networks for Event-Based Temporal Modeling and Beyond

We present Parametric Piecewise Linear Networks (PPLNs) for temporal vision inference. Motivated by the neuromorphic principles that regulate biological neural behaviors, PPLNs are ideal for processing data captured by event cameras, which are built to simulate neural activities in the human retina. We discuss how to represent the membrane potential of an artificial neuron by a parametric piecewise linear function with learnable coefficients. This design echoes the idea of building deep models from learnable parametric functions recently popularized by Kolmogorov-Arnold Networks (KANs). Experiments demonstrate the state-of-the-art performance of PPLNs in event-based and image-based vision applications, including steering prediction, human pose estimation, and motion deblurring. The source code of our implementation is available at https://github.com/chensong1995/PPLN.

Learning Transformation Synchronization

Reconstructing the 3D model of a physical object typically requires us to align the depth scans obtained from different camera poses into the same coordinate system. Solutions to this global alignment problem usually proceed in two steps. The first step estimates relative transformations between pairs of scans using an off-the-shelf technique. Due to limited information presented between pairs of scans, the resulting relative transformations are generally noisy. The second step then jointly optimizes the relative transformations among all input depth scans. A natural constraint used in this step is the cycle-consistency constraint, which allows us to prune incorrect relative transformations by detecting inconsistent cycles. The performance of such approaches, however, heavily relies on the quality of the input relative transformations. Instead of merely using the relative transformations as the input to perform transformation synchronization, we propose to use a neural network to learn the weights associated with each relative transformation. Our approach alternates between transformation synchronization using weighted relative transformations and predicting new weights of the input relative transformations using a neural network. We demonstrate the usefulness of this approach across a wide range of datasets.

Path-Invariant Map Networks

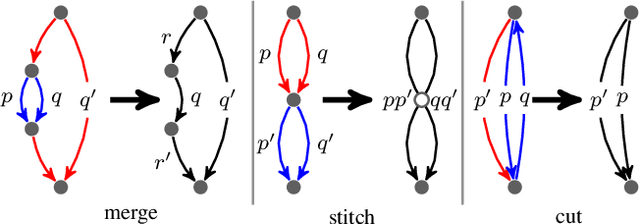
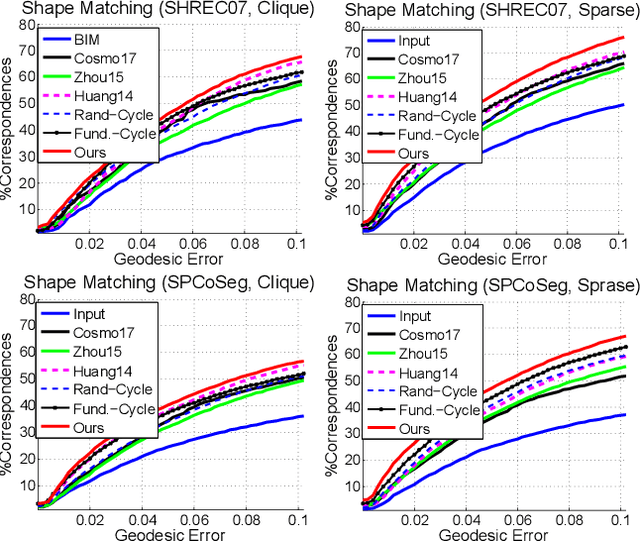
Optimizing a network of maps among a collection of objects/domains (or map synchronization) is a central problem across computer vision and many other relevant fields. Compared to optimizing pairwise maps in isolation, the benefit of map synchronization is that there are natural constraints among a map network that can improve the quality of individual maps. While such self-supervision constraints are well-understood for undirected map networks (e.g., the cycle-consistency constraint), they are under-explored for directed map networks, which naturally arise when maps are given by parametric maps (e.g., a feed-forward neural network). In this paper, we study a natural self-supervision constraint for directed map networks called path-invariance, which enforces that composite maps along different paths between a fixed pair of source and target domains are identical. We introduce path-invariance bases for efficient encoding of the path-invariance constraint and present an algorithm that outputs a path-variance basis with polynomial time and space complexities. We demonstrate the effectiveness of our formulation on optimizing object correspondences, estimating dense image maps via neural networks, and 3D scene segmentation via map networks of diverse 3D representations. In particular, our approach only requires 8% labeled data from ScanNet to achieve the same performance as training a single 3D segmentation network with 30% to 100% labeled data.