Zhengping Qian
G-Boost: Boosting Private SLMs with General LLMs
Mar 13, 2025Abstract:Due to the limited computational resources, most Large Language Models (LLMs) developers can only fine-tune Small Language Models (SLMs) on their own data. These private SLMs typically have limited effectiveness. To boost the performance of private SLMs, this paper proposes to ask general LLMs for help. The general LLMs can be APIs or larger LLMs whose inference cost the developers can afford. Specifically, we propose the G-Boost framework where a private SLM adaptively performs collaborative inference with a general LLM under the guide of process reward. Experiments demonstrate that our framework can significantly boost the performance of private SLMs.
Cardinality Estimation in DBMS: A Comprehensive Benchmark Evaluation
Sep 15, 2021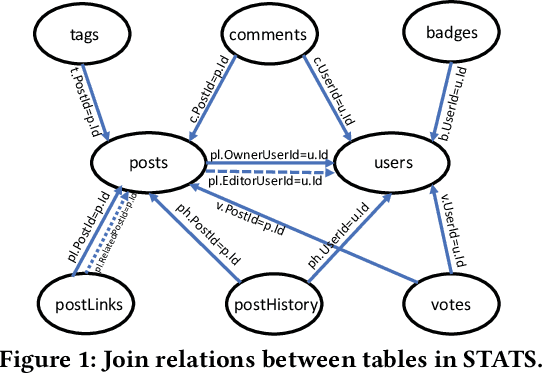
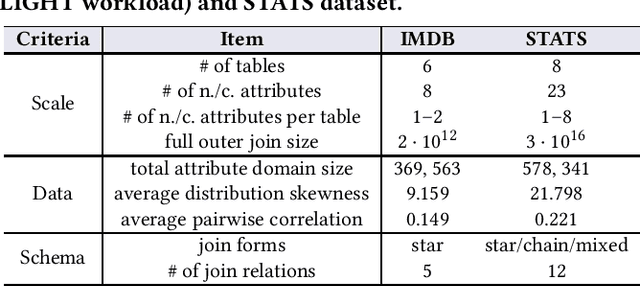
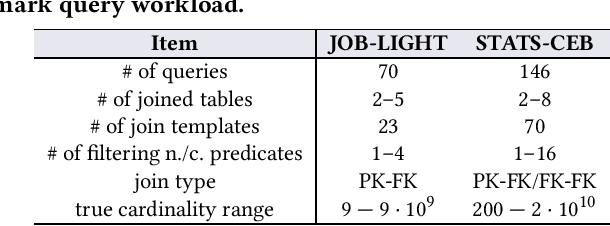
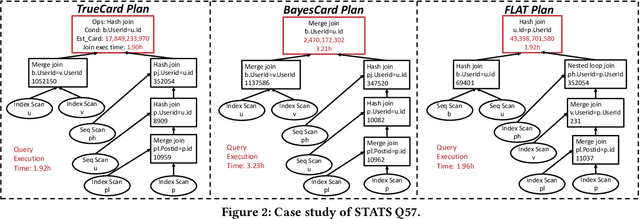
Abstract:Cardinality estimation (CardEst) plays a significant role in generating high-quality query plans for a query optimizer in DBMS. In the last decade, an increasing number of advanced CardEst methods (especially ML-based) have been proposed with outstanding estimation accuracy and inference latency. However, there exists no study that systematically evaluates the quality of these methods and answer the fundamental problem: to what extent can these methods improve the performance of query optimizer in real-world settings, which is the ultimate goal of a CardEst method. In this paper, we comprehensively and systematically compare the effectiveness of CardEst methods in a real DBMS. We establish a new benchmark for CardEst, which contains a new complex real-world dataset STATS and a diverse query workload STATS-CEB. We integrate multiple most representative CardEst methods into an open-source database system PostgreSQL, and comprehensively evaluate their true effectiveness in improving query plan quality, and other important aspects affecting their applicability, ranging from inference latency, model size, and training time, to update efficiency and accuracy. We obtain a number of key findings for the CardEst methods, under different data and query settings. Furthermore, we find that the widely used estimation accuracy metric(Q-Error) cannot distinguish the importance of different sub-plan queries during query optimization and thus cannot truly reflect the query plan quality generated by CardEst methods. Therefore, we propose a new metric P-Error to evaluate the performance of CardEst methods, which overcomes the limitation of Q-Error and is able to reflect the overall end-to-end performance of CardEst methods. We have made all of the benchmark data and evaluation code publicly available at https://github.com/Nathaniel-Han/End-to-End-CardEst-Benchmark.
FSPN: A New Class of Probabilistic Graphical Model
Nov 20, 2020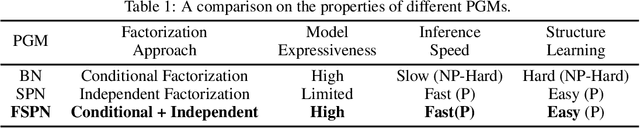
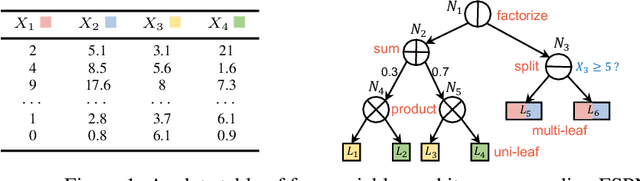
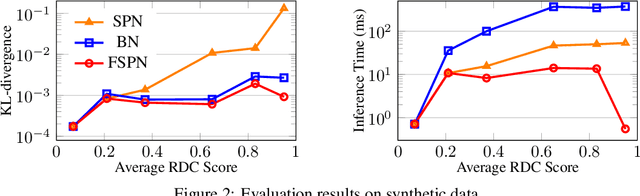
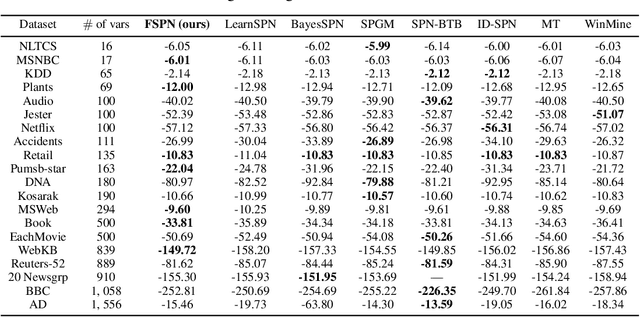
Abstract:We introduce factorize sum split product networks (FSPNs), a new class of probabilistic graphical models (PGMs). FSPNs are designed to overcome the drawbacks of existing PGMs in terms of estimation accuracy and inference efficiency. Specifically, Bayesian networks (BNs) have low inference speed and performance of tree structured sum product networks(SPNs) significantly degrades in presence of highly correlated variables. FSPNs absorb their advantages by adaptively modeling the joint distribution of variables according to their dependence degree, so that one can simultaneously attain the two desirable goals: high estimation accuracy and fast inference speed. We present efficient probability inference and structure learning algorithms for FSPNs, along with a theoretical analysis and extensive evaluation evidence. Our experimental results on synthetic and benchmark datasets indicate the superiority of FSPN over other PGMs.
FLAT: Fast, Lightweight and Accurate Method for Cardinality Estimation
Nov 18, 2020



Abstract:Query optimizers rely on accurate cardinality estimation (CardEst) to produce good execution plans. The core problem of CardEst is how to model the rich joint distribution of attributes in an accurate and compact manner. Despite decades of research, existing methods either over simplify the models only using independent factorization which leads to inaccurate estimates and sub optimal query plans, or over-complicate them by lossless conditional factorization without any independent assumption which results in slow probability computation. In this paper, we propose FLAT, a CardEst method that is simultaneously fast in probability computation, lightweight in model size and accurate in estimation quality. The key idea of FLAT is a novel unsupervised graphical model, called FSPN. It utilizes both independent and conditional factorization to adaptively model different levels of attributes correlations, and thus subsumes all existing CardEst models and dovetails their advantages. FLAT supports efficient online probability computation in near liner time on the underlying FSPN model, and provides effective offline model construction. It can estimate cardinality for both single table queries and multi-table join queries. Extensive experimental study demonstrates the superiority of FLAT over existing CardEst methods on well-known benchmarks: FLAT achieves 1 to 5 orders of magnitude better accuracy, 1 to 3 orders of magnitude faster probability computation speed (around 0.2ms) and 1 to 2 orders of magnitude lower storage cost (only tens of KB).
Taming the Expressiveness and Programmability of Graph Analytical Queries
Apr 20, 2020


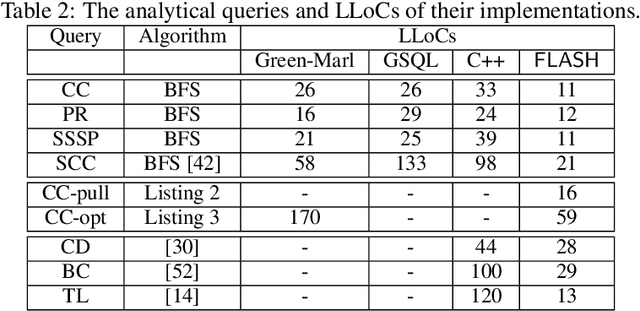
Abstract:Graph database has enjoyed a boom in the last decade, and graph queries accordingly gain a lot of attentions from both the academia and industry. We focus on analytical queries in this paper. While analyzing existing domain-specific languages (DSLs) for analytical queries regarding the perspectives of completeness, expressiveness and programmability, we find out that none of existing work has achieved a satisfactory coverage of these perspectives. Motivated by this, we propose the \flash DSL, which is named after the three primitive operators Filter, LocAl and PuSH. We prove that \flash is Turing complete (completeness), and show that it achieves both good expressiveness and programmability for analytical queries. We provide an implementation of \flash based on code generation, and compare it with native C++ codes and existing DSL using representative queries. The experiment results demonstrate \flash's expressiveness, and its capability of programming complex algorithms that achieve satisfactory runtime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge