PolyVivid: Vivid Multi-Subject Video Generation with Cross-Modal Interaction and Enhancement

Despite recent advances in video generation, existing models still lack fine-grained controllability, especially for multi-subject customization with consistent identity and interaction. In this paper, we propose PolyVivid, a multi-subject video customization framework that enables flexible and identity-consistent generation. To establish accurate correspondences between subject images and textual entities, we design a VLLM-based text-image fusion module that embeds visual identities into the textual space for precise grounding. To further enhance identity preservation and subject interaction, we propose a 3D-RoPE-based enhancement module that enables structured bidirectional fusion between text and image embeddings. Moreover, we develop an attention-inherited identity injection module to effectively inject fused identity features into the video generation process, mitigating identity drift. Finally, we construct an MLLM-based data pipeline that combines MLLM-based grounding, segmentation, and a clique-based subject consolidation strategy to produce high-quality multi-subject data, effectively enhancing subject distinction and reducing ambiguity in downstream video generation. Extensive experiments demonstrate that PolyVivid achieves superior performance in identity fidelity, video realism, and subject alignment, outperforming existing open-source and commercial baselines.

HunyuanCustom: A Multimodal-Driven Architecture for Customized Video Generation

Customized video generation aims to produce videos featuring specific subjects under flexible user-defined conditions, yet existing methods often struggle with identity consistency and limited input modalities. In this paper, we propose HunyuanCustom, a multi-modal customized video generation framework that emphasizes subject consistency while supporting image, audio, video, and text conditions. Built upon HunyuanVideo, our model first addresses the image-text conditioned generation task by introducing a text-image fusion module based on LLaVA for enhanced multi-modal understanding, along with an image ID enhancement module that leverages temporal concatenation to reinforce identity features across frames. To enable audio- and video-conditioned generation, we further propose modality-specific condition injection mechanisms: an AudioNet module that achieves hierarchical alignment via spatial cross-attention, and a video-driven injection module that integrates latent-compressed conditional video through a patchify-based feature-alignment network. Extensive experiments on single- and multi-subject scenarios demonstrate that HunyuanCustom significantly outperforms state-of-the-art open- and closed-source methods in terms of ID consistency, realism, and text-video alignment. Moreover, we validate its robustness across downstream tasks, including audio and video-driven customized video generation. Our results highlight the effectiveness of multi-modal conditioning and identity-preserving strategies in advancing controllable video generation. All the code and models are available at https://hunyuancustom.github.io.

InstantCharacter: Personalize Any Characters with a Scalable Diffusion Transformer Framework

Current learning-based subject customization approaches, predominantly relying on U-Net architectures, suffer from limited generalization ability and compromised image quality. Meanwhile, optimization-based methods require subject-specific fine-tuning, which inevitably degrades textual controllability. To address these challenges, we propose InstantCharacter, a scalable framework for character customization built upon a foundation diffusion transformer. InstantCharacter demonstrates three fundamental advantages: first, it achieves open-domain personalization across diverse character appearances, poses, and styles while maintaining high-fidelity results. Second, the framework introduces a scalable adapter with stacked transformer encoders, which effectively processes open-domain character features and seamlessly interacts with the latent space of modern diffusion transformers. Third, to effectively train the framework, we construct a large-scale character dataset containing 10-million-level samples. The dataset is systematically organized into paired (multi-view character) and unpaired (text-image combinations) subsets. This dual-data structure enables simultaneous optimization of identity consistency and textual editability through distinct learning pathways. Qualitative experiments demonstrate the advanced capabilities of InstantCharacter in generating high-fidelity, text-controllable, and character-consistent images, setting a new benchmark for character-driven image generation. Our source code is available at https://github.com/Tencent/InstantCharacter.

Online Filter Clustering and Pruning for Efficient Convnets

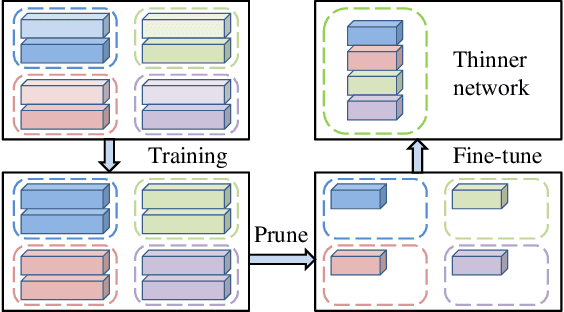
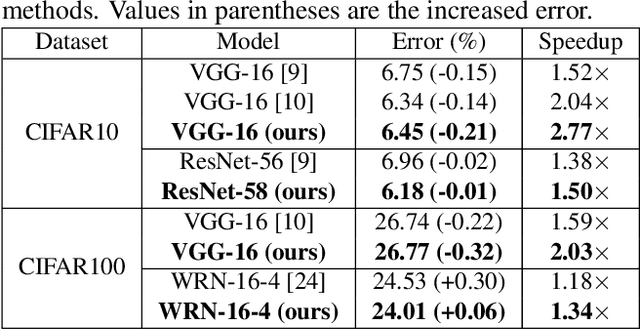
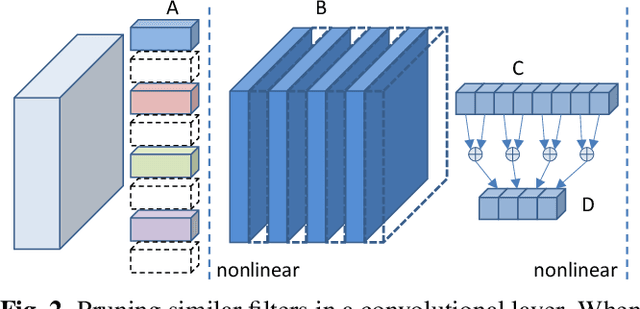
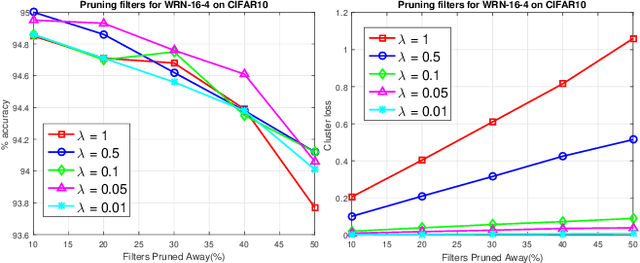
Pruning filters is an effective method for accelerating deep neural networks (DNNs), but most existing approaches prune filters on a pre-trained network directly which limits in acceleration. Although each filter has its own effect in DNNs, but if two filters are the same with each other, we could prune one safely. In this paper, we add an extra cluster loss term in the loss function which can force filters in each cluster to be similar online. After training, we keep one filter in each cluster and prune others and fine-tune the pruned network to compensate for the loss. Particularly, the clusters in every layer can be defined firstly which is effective for pruning DNNs within residual blocks. Extensive experiments on CIFAR10 and CIFAR100 benchmarks demonstrate the competitive performance of our proposed filter pruning method.

Progressive Learning of Low-Precision Networks

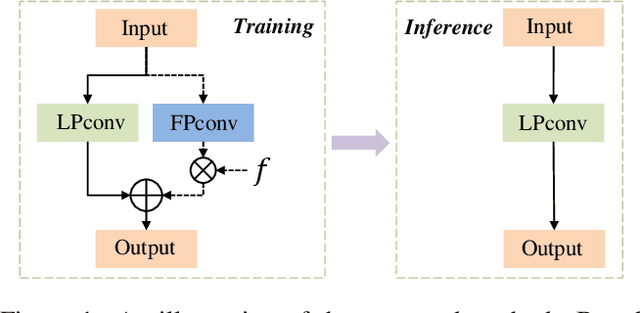
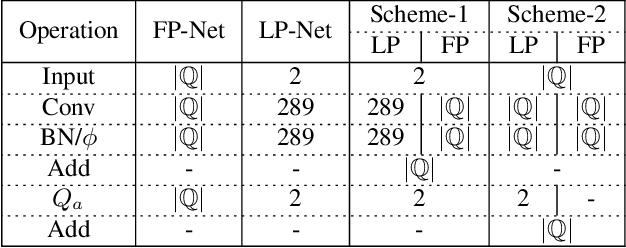
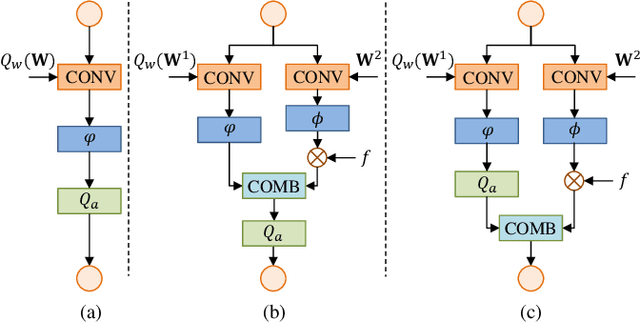
Recent years have witnessed the great advance of deep learning in a variety of vision tasks. Many state-of-the-art deep neural networks suffer from large size and high complexity, which makes it difficult to deploy in resource-limited platforms such as mobile devices. To this end, low-precision neural networks are widely studied which quantize weights or activations into the low-bit format. Though being efficient, low-precision networks are usually hard to train and encounter severe accuracy degradation. In this paper, we propose a new training strategy through expanding low-precision networks during training and removing the expanded parts for network inference. First, we equip each low-precision convolutional layer with an ancillary full-precision convolutional layer based on a low-precision network structure, which could guide the network to good local minima. Second, a decay method is introduced to reduce the output of the added full-precision convolution gradually, which keeps the resulted topology structure the same to the original low-precision one. Experiments on SVHN, CIFAR and ILSVRC-2012 datasets prove that the proposed method can bring faster convergence and higher accuracy for low-precision neural networks.