MEGA: A Memory-Efficient GNN Accelerator Exploiting Degree-Aware Mixed-Precision Quantization

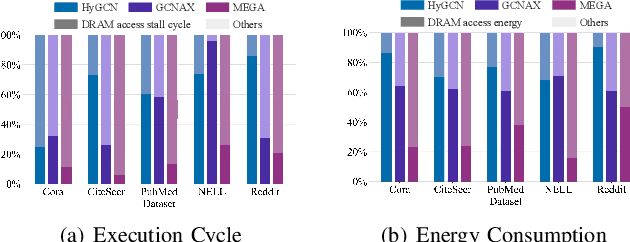
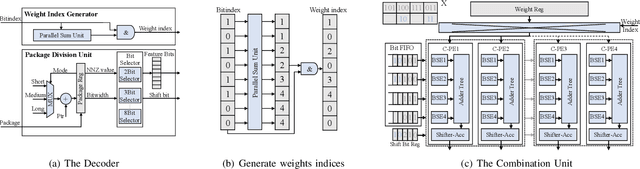
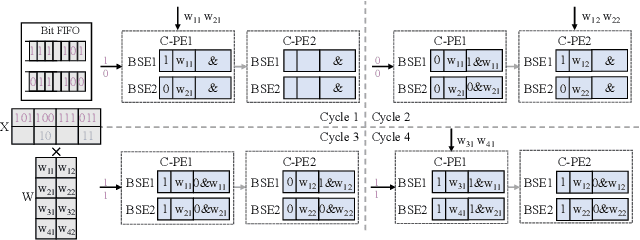
Graph Neural Networks (GNNs) are becoming a promising technique in various domains due to their excellent capabilities in modeling non-Euclidean data. Although a spectrum of accelerators has been proposed to accelerate the inference of GNNs, our analysis demonstrates that the latency and energy consumption induced by DRAM access still significantly impedes the improvement of performance and energy efficiency. To address this issue, we propose a Memory-Efficient GNN Accelerator (MEGA) through algorithm and hardware co-design in this work. Specifically, at the algorithm level, through an in-depth analysis of the node property, we observe that the data-independent quantization in previous works is not optimal in terms of accuracy and memory efficiency. This motivates us to propose the Degree-Aware mixed-precision quantization method, in which a proper bitwidth is learned and allocated to a node according to its in-degree to compress GNNs as much as possible while maintaining accuracy. At the hardware level, we employ a heterogeneous architecture design in which the aggregation and combination phases are implemented separately with different dataflows. In order to boost the performance and energy efficiency, we also present an Adaptive-Package format to alleviate the storage overhead caused by the fine-grained bitwidth and diverse sparsity, and a Condense-Edge scheduling method to enhance the data locality and further alleviate the access irregularity induced by the extremely sparse adjacency matrix in the graph. We implement our MEGA accelerator in a 28nm technology node. Extensive experiments demonstrate that MEGA can achieve an average speedup of 38.3x, 7.1x, 4.0x, 3.6x and 47.6x, 7.2x, 5.4x, 4.5x energy savings over four state-of-the-art GNN accelerators, HyGCN, GCNAX, GROW, and SGCN, respectively, while retaining task accuracy.

$\rm A^2Q$: Aggregation-Aware Quantization for Graph Neural Networks

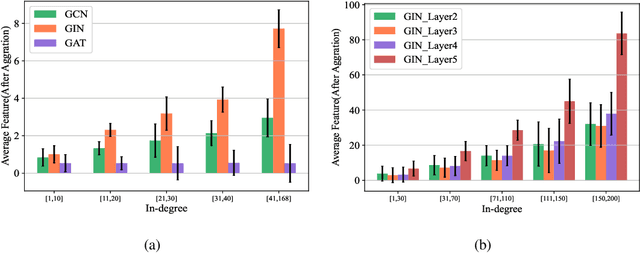
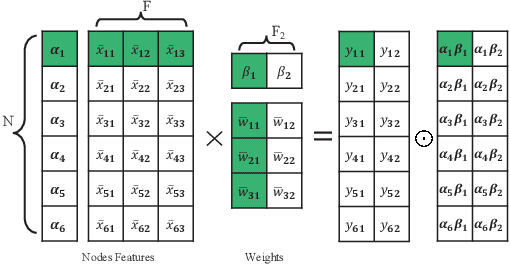
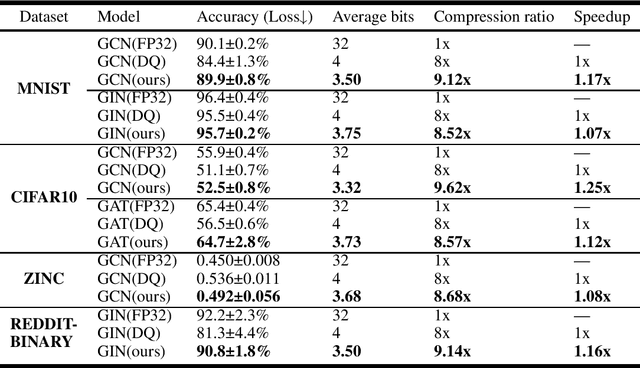
As graph data size increases, the vast latency and memory consumption during inference pose a significant challenge to the real-world deployment of Graph Neural Networks (GNNs). While quantization is a powerful approach to reducing GNNs complexity, most previous works on GNNs quantization fail to exploit the unique characteristics of GNNs, suffering from severe accuracy degradation. Through an in-depth analysis of the topology of GNNs, we observe that the topology of the graph leads to significant differences between nodes, and most of the nodes in a graph appear to have a small aggregation value. Motivated by this, in this paper, we propose the Aggregation-Aware mixed-precision Quantization ($\rm A^2Q$) for GNNs, where an appropriate bitwidth is automatically learned and assigned to each node in the graph. To mitigate the vanishing gradient problem caused by sparse connections between nodes, we propose a Local Gradient method to serve the quantization error of the node features as the supervision during training. We also develop a Nearest Neighbor Strategy to deal with the generalization on unseen graphs. Extensive experiments on eight public node-level and graph-level datasets demonstrate the generality and robustness of our proposed method. Compared to the FP32 models, our method can achieve up to a 18.6x (i.e., 1.70bit) compression ratio with negligible accuracy degradation. Morever, compared to the state-of-the-art quantization method, our method can achieve up to 11.4\% and 9.5\% accuracy improvements on the node-level and graph-level tasks, respectively, and up to 2x speedup on a dedicated hardware accelerator.

Hardware Acceleration of Fully Quantized BERT for Efficient Natural Language Processing

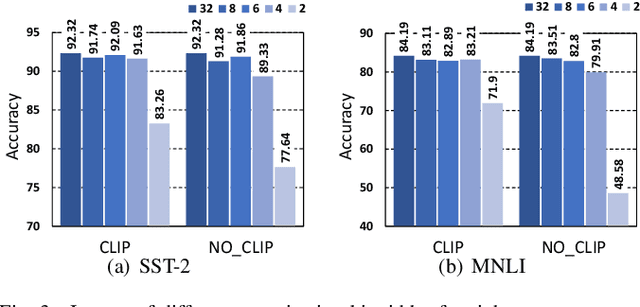
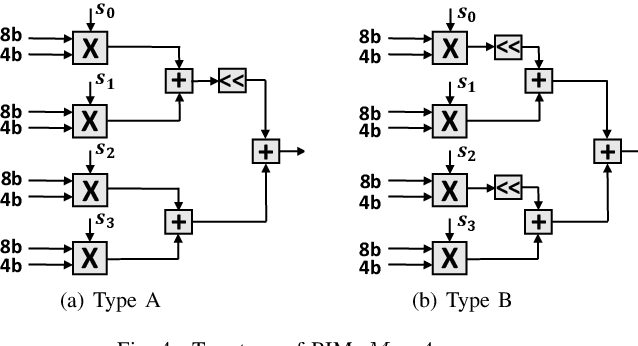
BERT is the most recent Transformer-based model that achieves state-of-the-art performance in various NLP tasks. In this paper, we investigate the hardware acceleration of BERT on FPGA for edge computing. To tackle the issue of huge computational complexity and memory footprint, we propose to fully quantize the BERT (FQ-BERT), including weights, activations, softmax, layer normalization, and all the intermediate results. Experiments demonstrate that the FQ-BERT can achieve 7.94x compression for weights with negligible performance loss. We then propose an accelerator tailored for the FQ-BERT and evaluate on Xilinx ZCU102 and ZCU111 FPGA. It can achieve a performance-per-watt of 3.18 fps/W, which is 28.91x and 12.72x over Intel(R) Core(TM) i7-8700 CPU and NVIDIA K80 GPU, respectively.

Equivalence of Convergence Rates of Posterior Distributions and Bayes Estimators for Functions and Nonparametric Functionals

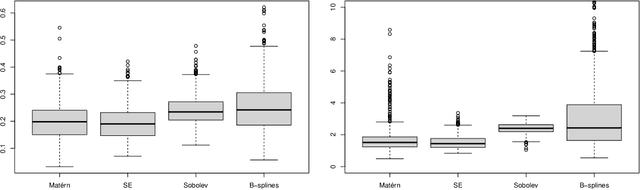
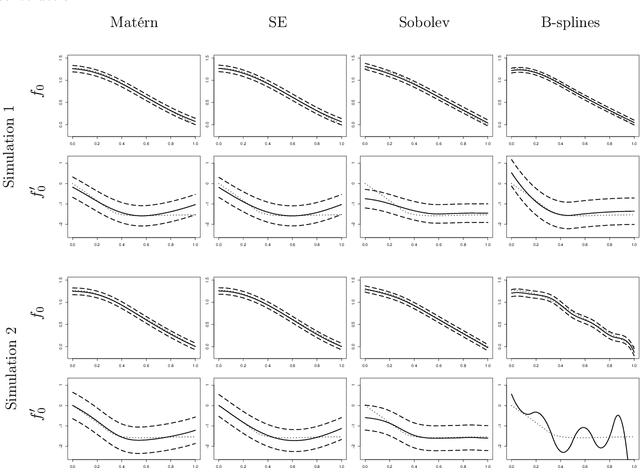
We study the posterior contraction rates of a Bayesian method with Gaussian process priors in nonparametric regression and its plug-in property for differential operators. For a general class of kernels, we establish convergence rates of the posterior measure of the regression function and its derivatives, which are both minimax optimal up to a logarithmic factor for functions in certain classes. Our calculation shows that the rate-optimal estimation of the regression function and its derivatives share the same choice of hyperparameter, indicating that the Bayes procedure remarkably adapts to the order of derivatives and enjoys a generalized plug-in property that extends real-valued functionals to function-valued functionals. This leads to a practically simple method for estimating the regression function and its derivatives, whose finite sample performance is assessed using simulations. Our proof shows that, under certain conditions, to any convergence rate of Bayes estimators there corresponds the same convergence rate of the posterior distributions (i.e., posterior contraction rate), and vice versa. This equivalence holds for a general class of Gaussian processes and covers the regression function and its derivative functionals, under both the $L_2$ and $L_{\infty}$ norms. In addition to connecting these two fundamental large sample properties in Bayesian and non-Bayesian regimes, such equivalence enables a new routine to establish posterior contraction rates by calculating convergence rates of nonparametric point estimators. At the core of our argument is an operator-theoretic framework for kernel ridge regression and equivalent kernel techniques. We derive a range of sharp non-asymptotic bounds that are pivotal in establishing convergence rates of nonparametric point estimators and the equivalence theory, which may be of independent interest.

Non-asymptotic Analysis in Kernel Ridge Regression

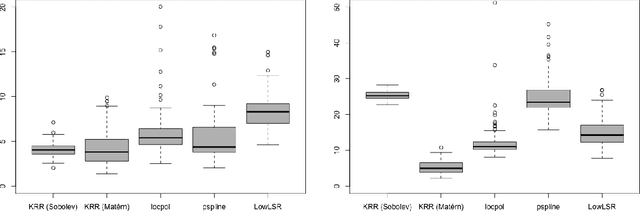
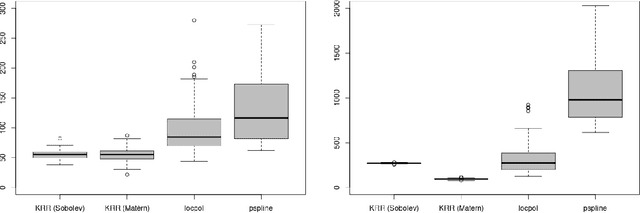
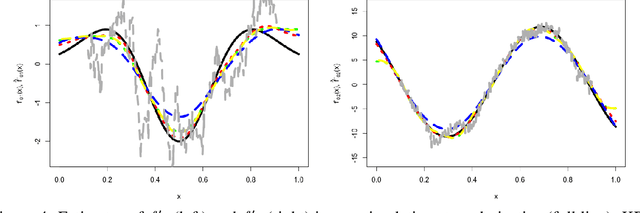
We develop a general non-asymptotic analysis of learning rates in kernel ridge regression (KRR), applicable for arbitrary Mercer kernels with multi-dimensional support. Our analysis is based on an operator-theoretic framework, at the core of which lies two error bounds under reproducing kernel Hilbert space norms encompassing a general class of kernels and regression functions, with remarkable extensibility to various inferential goals through augmenting results. When applied to KRR estimators, our analysis leads to error bounds under the stronger supremum norm, in addition to the commonly studied weighted $L_2$ norm; in a concrete example specialized to the Mat\'ern kernel, the established bounds recover the nearly minimax optimal rates. The wide applicability of our analysis is further demonstrated through two new theoretical results: (1) non-asymptotic learning rates for mixed partial derivatives of KRR estimators, and (2) a non-asymptotic characterization of the posterior variances of Gaussian processes, which corresponds to uncertainty quantification in kernel methods and nonparametric Bayes.

A System-Level Solution for Low-Power Object Detection

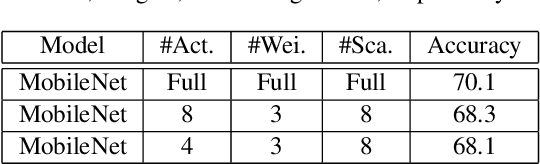
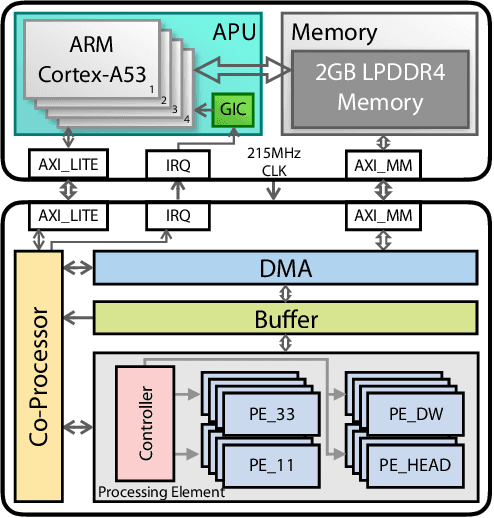
Object detection has made impressive progress in recent years with the help of deep learning. However, state-of-the-art algorithms are both computation and memory intensive. Though many lightweight networks are developed for a trade-off between accuracy and efficiency, it is still a challenge to make it practical on an embedded device. In this paper, we present a system-level solution for efficient object detection on a heterogeneous embedded device. The detection network is quantized to low bits and allows efficient implementation with shift operators. In order to make the most of the benefits of low-bit quantization, we design a dedicated accelerator with programmable logic. Inside the accelerator, a hybrid dataflow is exploited according to the heterogeneous property of different convolutional layers. We adopt a straightforward but resource-friendly column-prior tiling strategy to map the computation-intensive convolutional layers to the accelerator that can support arbitrary feature size. Other operations can be performed on the low-power CPU cores, and the entire system is executed in a pipelined manner. As a case study, we evaluate our object detection system on a real-world surveillance video with input size of 512x512, and it turns out that the system can achieve an inference speed of 18 fps at the cost of 6.9W (with display) with an mAP of 66.4 verified on the PASCAL VOC 2012 dataset.