Non-asymptotic Analysis in Kernel Ridge Regression

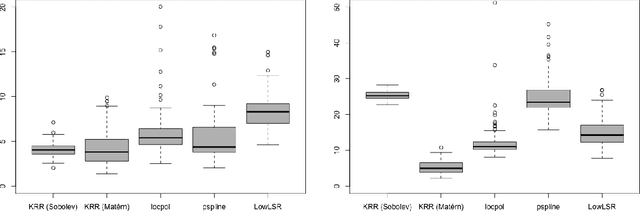
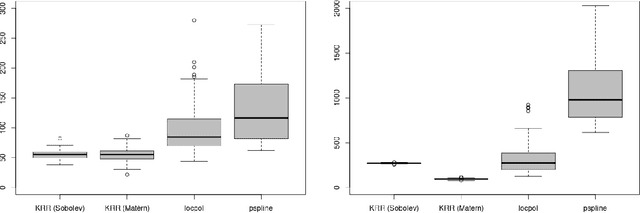
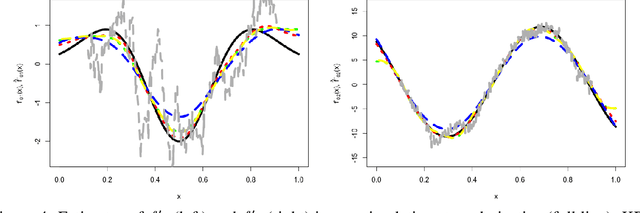
We develop a general non-asymptotic analysis of learning rates in kernel ridge regression (KRR), applicable for arbitrary Mercer kernels with multi-dimensional support. Our analysis is based on an operator-theoretic framework, at the core of which lies two error bounds under reproducing kernel Hilbert space norms encompassing a general class of kernels and regression functions, with remarkable extensibility to various inferential goals through augmenting results. When applied to KRR estimators, our analysis leads to error bounds under the stronger supremum norm, in addition to the commonly studied weighted $L_2$ norm; in a concrete example specialized to the Mat\'ern kernel, the established bounds recover the nearly minimax optimal rates. The wide applicability of our analysis is further demonstrated through two new theoretical results: (1) non-asymptotic learning rates for mixed partial derivatives of KRR estimators, and (2) a non-asymptotic characterization of the posterior variances of Gaussian processes, which corresponds to uncertainty quantification in kernel methods and nonparametric Bayes.