UNOC: Understanding Occlusion for Embodied Presence in Virtual Reality

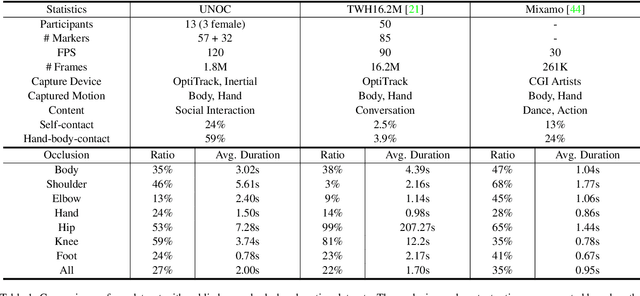
Tracking body and hand motions in the 3D space is essential for social and self-presence in augmented and virtual environments. Unlike the popular 3D pose estimation setting, the problem is often formulated as inside-out tracking based on embodied perception (e.g., egocentric cameras, handheld sensors). In this paper, we propose a new data-driven framework for inside-out body tracking, targeting challenges of omnipresent occlusions in optimization-based methods (e.g., inverse kinematics solvers). We first collect a large-scale motion capture dataset with both body and finger motions using optical markers and inertial sensors. This dataset focuses on social scenarios and captures ground truth poses under self-occlusions and body-hand interactions. We then simulate the occlusion patterns in head-mounted camera views on the captured ground truth using a ray casting algorithm and learn a deep neural network to infer the occluded body parts. In the experiments, we show that our method is able to generate high-fidelity embodied poses by applying the proposed method on the task of real-time inside-out body tracking, finger motion synthesis, and 3-point inverse kinematics.

Binary Stereo Matching

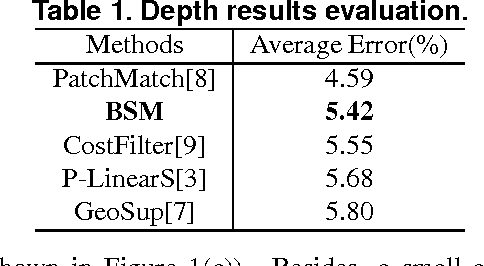
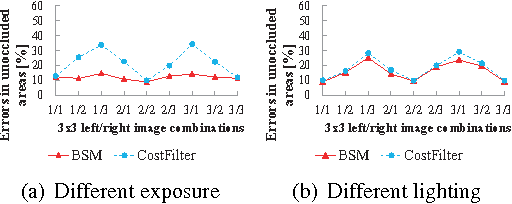
In this paper, we propose a novel binary-based cost computation and aggregation approach for stereo matching problem. The cost volume is constructed through bitwise operations on a series of binary strings. Then this approach is combined with traditional winner-take-all strategy, resulting in a new local stereo matching algorithm called binary stereo matching (BSM). Since core algorithm of BSM is based on binary and integer computations, it has a higher computational efficiency than previous methods. Experimental results on Middlebury benchmark show that BSM has comparable performance with state-of-the-art local stereo methods in terms of both quality and speed. Furthermore, experiments on images with radiometric differences demonstrate that BSM is more robust than previous methods under these changes, which is common under real illumination.

Solving Hybrid Influence Diagrams with Deterministic Variables

We describe a framework and an algorithm for solving hybrid influence diagrams with discrete, continuous, and deterministic chance variables, and discrete and continuous decision variables. A continuous chance variable in an influence diagram is said to be deterministic if its conditional distributions have zero variances. The solution algorithm is an extension of Shenoy's fusion algorithm for discrete influence diagrams. We describe an extended Shenoy-Shafer architecture for propagation of discrete, continuous, and utility potentials in hybrid influence diagrams that include deterministic chance variables. The algorithm and framework are illustrated by solving two small examples.