An Interval-Valued Utility Theory for Decision Making with Dempster-Shafer Belief Functions

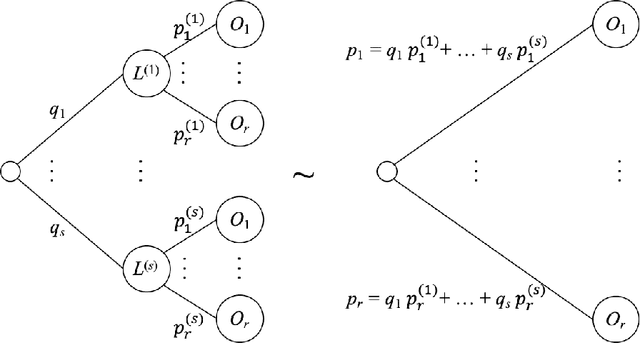
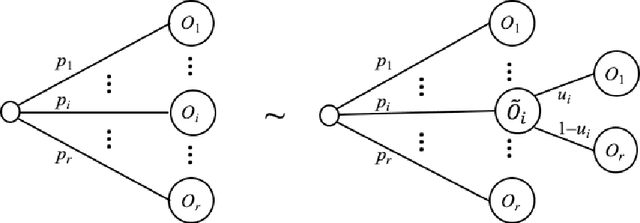
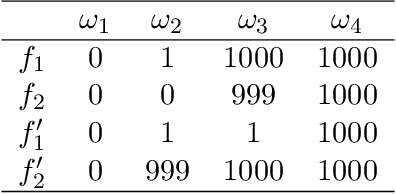
The main goal of this paper is to describe an axiomatic utility theory for Dempster-Shafer belief function lotteries. The axiomatic framework used is analogous to von Neumann-Morgenstern's utility theory for probabilistic lotteries as described by Luce and Raiffa. Unlike the probabilistic case, our axiomatic framework leads to interval-valued utilities, and therefore, to a partial (incomplete) preference order on the set of all belief function lotteries. If the belief function reference lotteries we use are Bayesian belief functions, then our representation theorem coincides with Jaffray's representation theorem for his linear utility theory for belief functions. We illustrate our framework using some examples discussed in the literature, and we propose a simple model based on an interval-valued pessimism index representing a decision-maker's attitude to ambiguity and indeterminacy. Finally, we compare our decision theory with those proposed by Jaffray, Smets, Dubois et al., Giang and Shenoy, and Shafer.

Propagation of Belief Functions: A Distributed Approach

In this paper, we describe a scheme for propagating belief functions in certain kinds of trees using only local computations. This scheme generalizes the computational scheme proposed by Shafer and Logan1 for diagnostic trees of the type studied by Gordon and Shortliffe, and the slightly more general scheme given by Shafer for hierarchical evidence. It also generalizes the scheme proposed by Pearl for Bayesian causal trees (see Shenoy and Shafer). Pearl's causal trees and Gordon and Shortliffe's diagnostic trees are both ways of breaking the evidence that bears on a large problem down into smaller items of evidence that bear on smaller parts of the problem so that these smaller problems can be dealt with one at a time. This localization of effort is often essential in order to make the process of probability judgment feasible, both for the person who is making probability judgments and for the machine that is combining them. The basic structure for our scheme is a type of tree that generalizes both Pearl's and Gordon and Shortliffe's trees. Trees of this general type permit localized computation in Pearl's sense. They are based on qualitative judgments of conditional independence. We believe that the scheme we describe here will prove useful in expert systems. It is now clear that the successful propagation of probabilities or certainty factors in expert systems requires much more structure than can be provided in a pure production-system framework. Bayesian schemes, on the other hand, often make unrealistic demands for structure. The propagation of belief functions in trees and more general networks stands on a middle ground where some sensible and useful things can be done. We would like to emphasize that the basic idea of local computation for propagating probabilities is due to Judea Pearl. It is a very innovative idea; we do not believe that it can be found in the Bayesian literature prior to Pearl's work. We see our contribution as extending the usefulness of Pearl's idea by generalizing it from Bayesian probabilities to belief functions. In the next section, we give a brief introduction to belief functions. The notions of qualitative independence for partitions and a qualitative Markov tree are introduced in Section III. Finally, in Section IV, we describe a scheme for propagating belief functions in qualitative Markov trees.

Modifiable Combining Functions

Modifiable combining functions are a synthesis of two common approaches to combining evidence. They offer many of the advantages of these approaches and avoid some disadvantages. Because they facilitate the acquisition, representation, explanation, and modification of knowledge about combinations of evidence, they are proposed as a tool for knowledge engineers who build systems that reason under uncertainty, not as a normative theory of evidence.

An Axiomatic Framework for Bayesian and Belief-function Propagation

In this paper, we describe an abstract framework and axioms under which exact local computation of marginals is possible. The primitive objects of the framework are variables and valuations. The primitive operators of the framework are combination and marginalization. These operate on valuations. We state three axioms for these operators and we derive the possibility of local computation from the axioms. Next, we describe a propagation scheme for computing marginals of a valuation when we have a factorization of the valuation on a hypertree. Finally we show how the problem of computing marginals of joint probability distributions and joint belief functions fits the general framework.

Valuation-Based Systems for Discrete Optimization

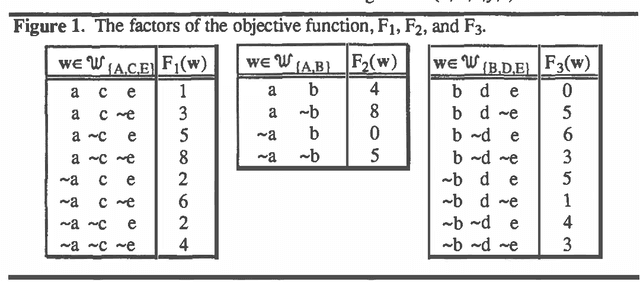
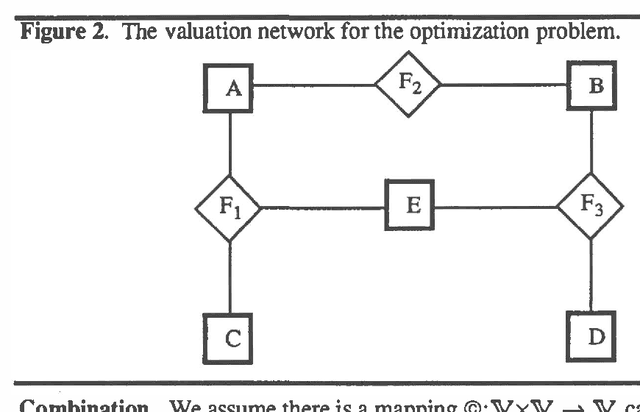
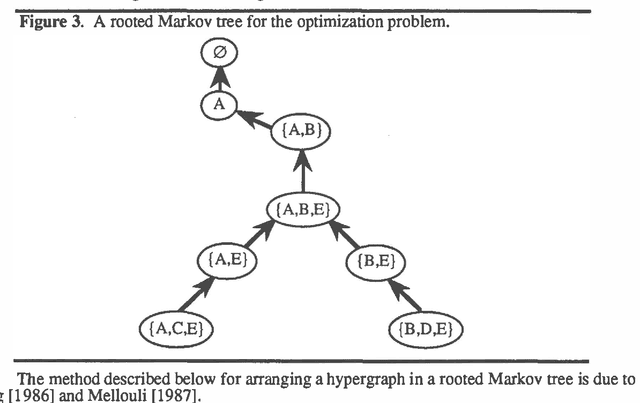
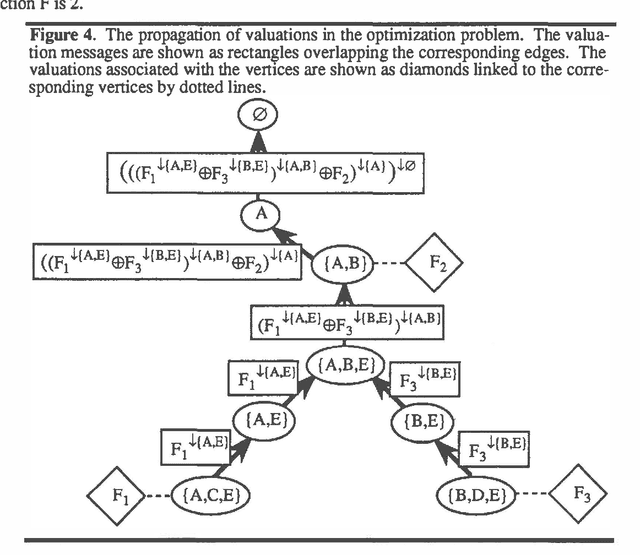
This paper describes valuation-based systems for representing and solving discrete optimization problems. In valuation-based systems, we represent information in an optimization problem using variables, sample spaces of variables, a set of values, and functions that map sample spaces of sets of variables to the set of values. The functions, called valuations, represent the factors of an objective function. Solving the optimization problem involves using two operations called combination and marginalization. Combination tells us how to combine the factors of the joint objective function. Marginalization is either maximization or minimization. Solving an optimization problem can be simply described as finding the marginal of the joint objective function for the empty set. We state some simple axioms that combination and marginalization need to satisfy to enable us to solve an optimization problem using local computation. For optimization problems, the solution method of valuation-based systems reduces to non-serial dynamic programming. Thus our solution method for VBS can be regarded as an abstract description of dynamic programming. And our axioms can be viewed as conditions that permit the use of dynamic programming.

A Fusion Algorithm for Solving Bayesian Decision Problems

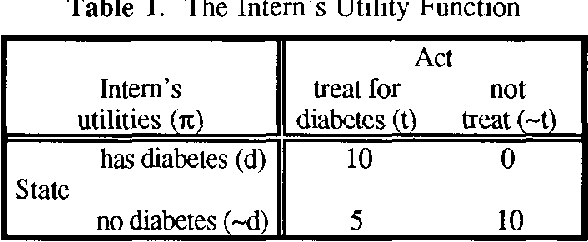
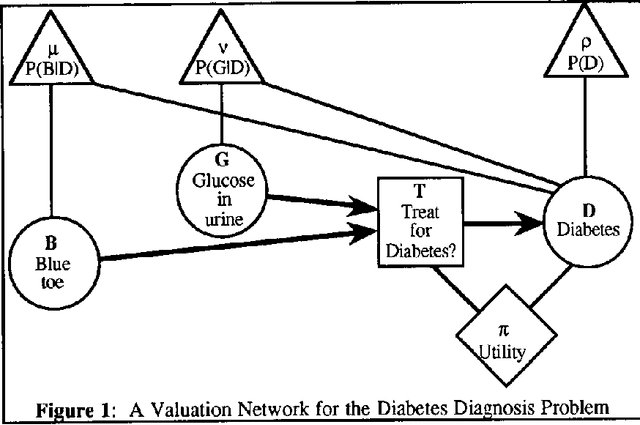
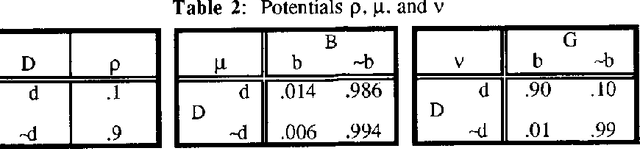
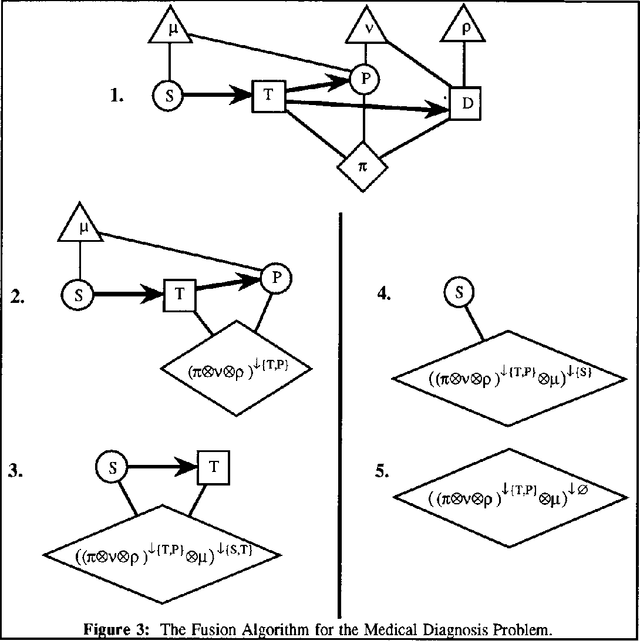
This paper proposes a new method for solving Bayesian decision problems. The method consists of representing a Bayesian decision problem as a valuation-based system and applying a fusion algorithm for solving it. The fusion algorithm is a hybrid of local computational methods for computation of marginals of joint probability distributions and the local computational methods for discrete optimization problems.

Conditional Independence in Uncertainty Theories

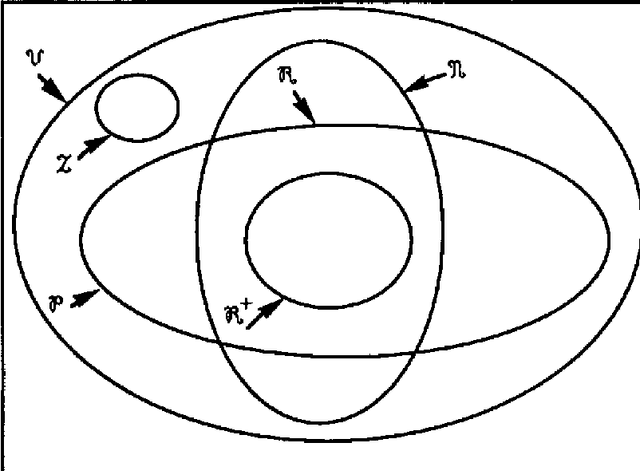
This paper introduces the notions of independence and conditional independence in valuation-based systems (VBS). VBS is an axiomatic framework capable of representing many different uncertainty calculi. We define independence and conditional independence in terms of factorization of the joint valuation. The definitions of independence and conditional independence in VBS generalize the corresponding definitions in probability theory. Our definitions apply not only to probability theory, but also to Dempster-Shafer's belief-function theory, Spohn's epistemic-belief theory, and Zadeh's possibility theory. In fact, they apply to any uncertainty calculi that fit in the framework of valuation-based systems.

Valuation Networks and Conditional Independence

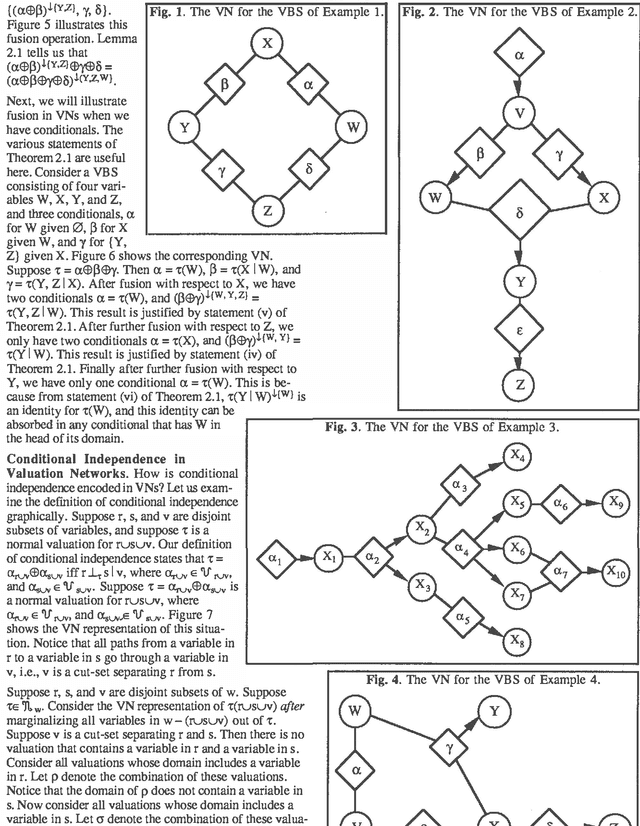
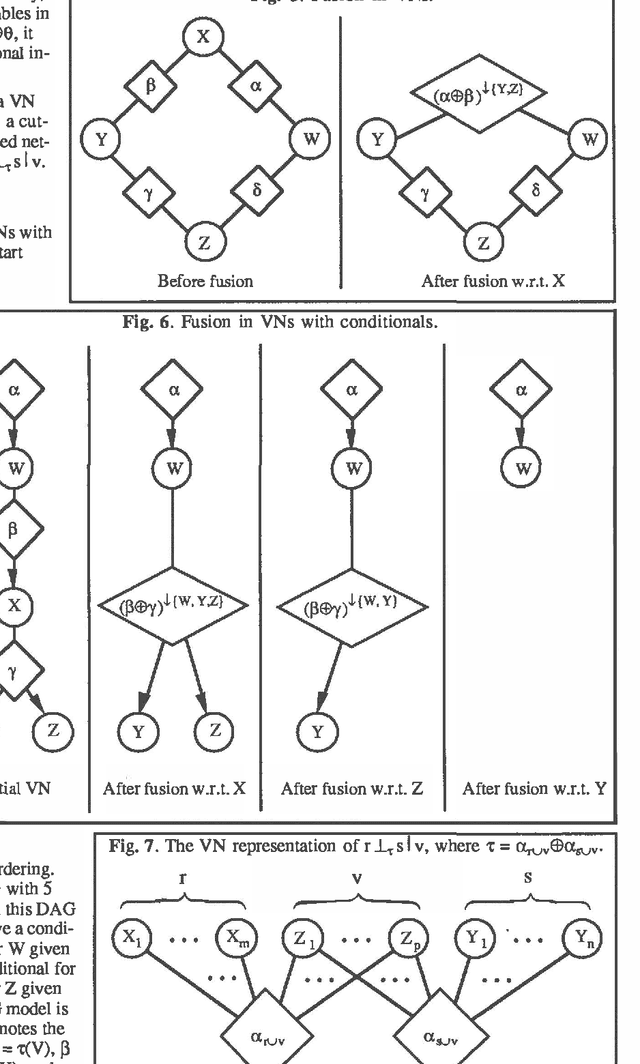
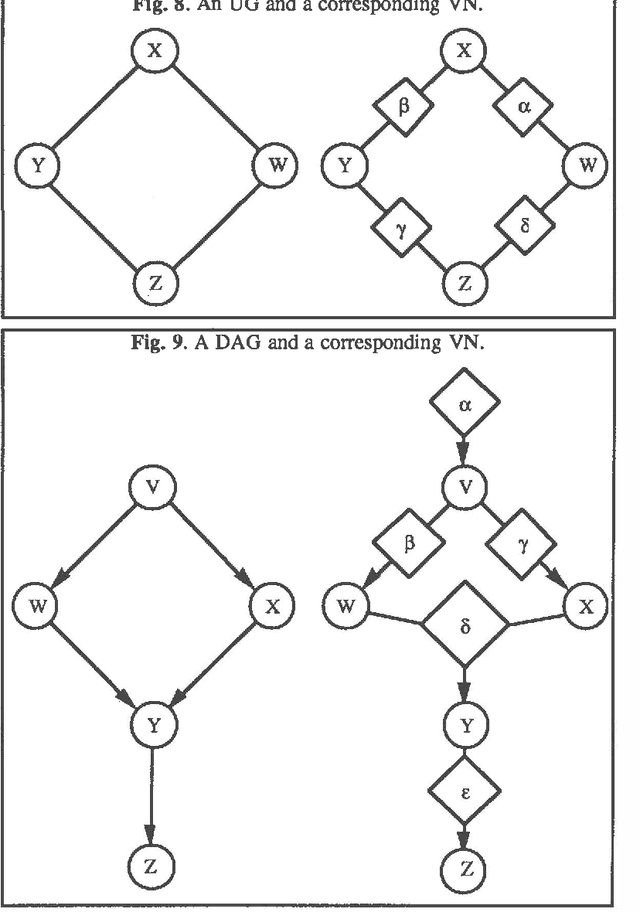
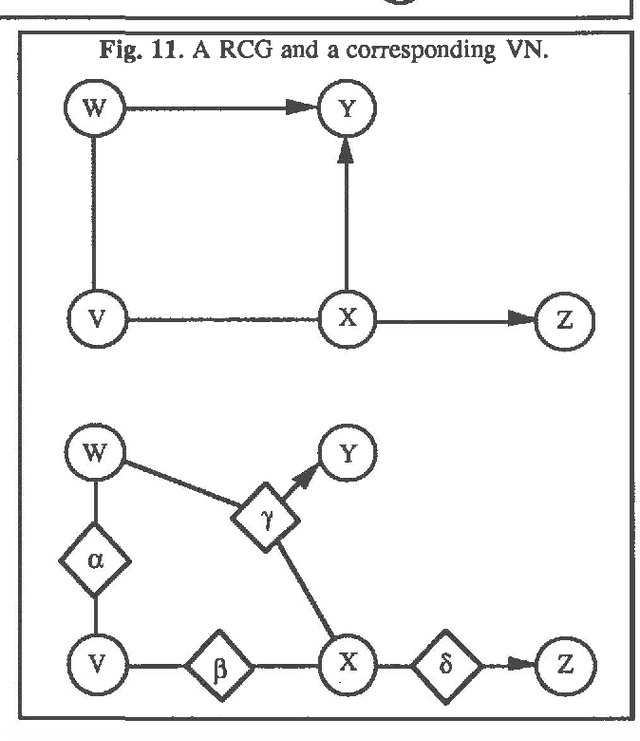
Valuation networks have been proposed as graphical representations of valuation-based systems (VBSs). The VBS framework is able to capture many uncertainty calculi including probability theory, Dempster-Shafer's belief-function theory, Spohn's epistemic belief theory, and Zadeh's possibility theory. In this paper, we show how valuation networks encode conditional independence relations. For the probabilistic case, the class of probability models encoded by valuation networks includes undirected graph models, directed acyclic graph models, directed balloon graph models, and recursive causal graph models.

A New Pruning Method for Solving Decision Trees and Game Trees

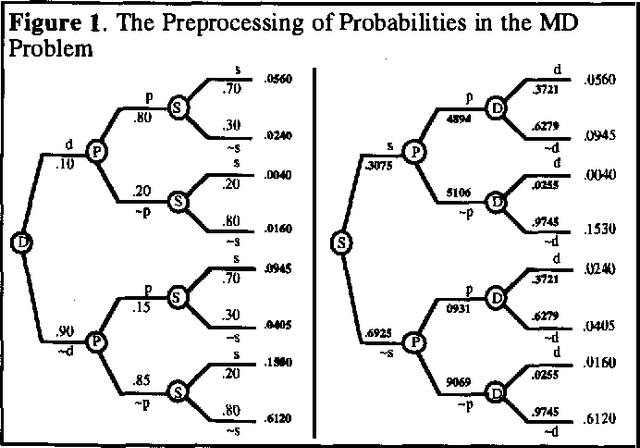
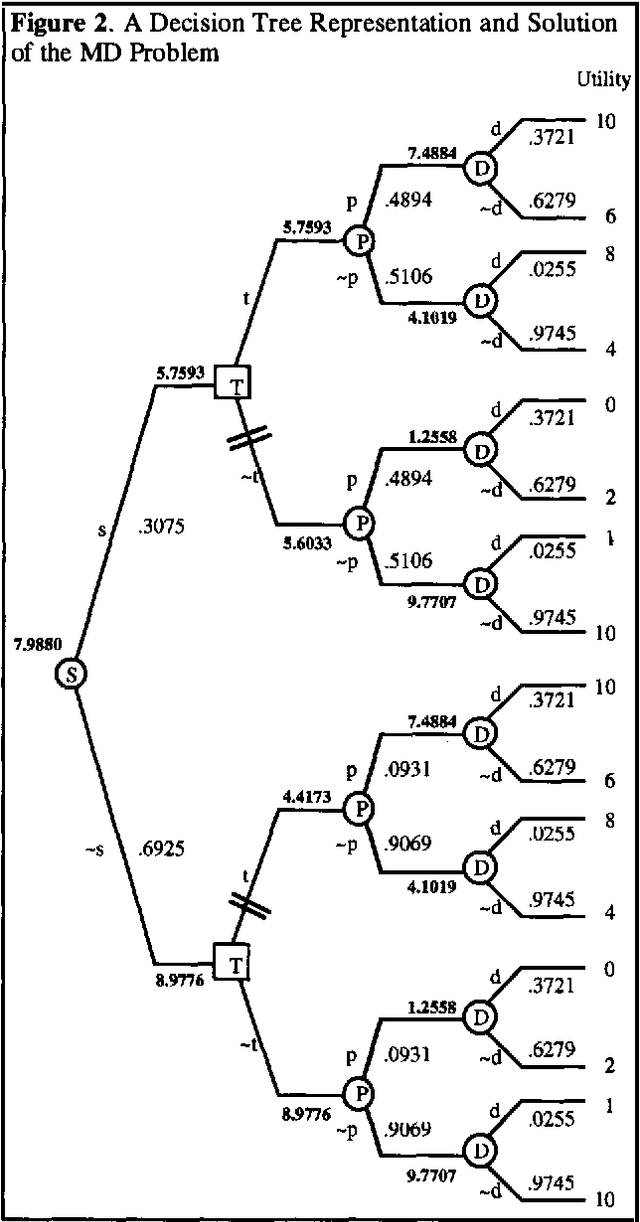
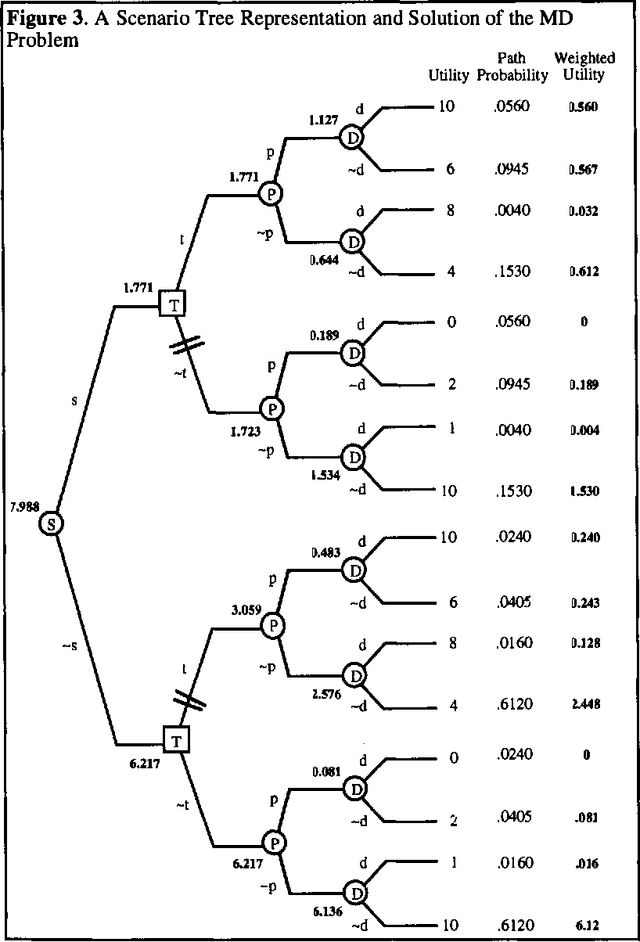
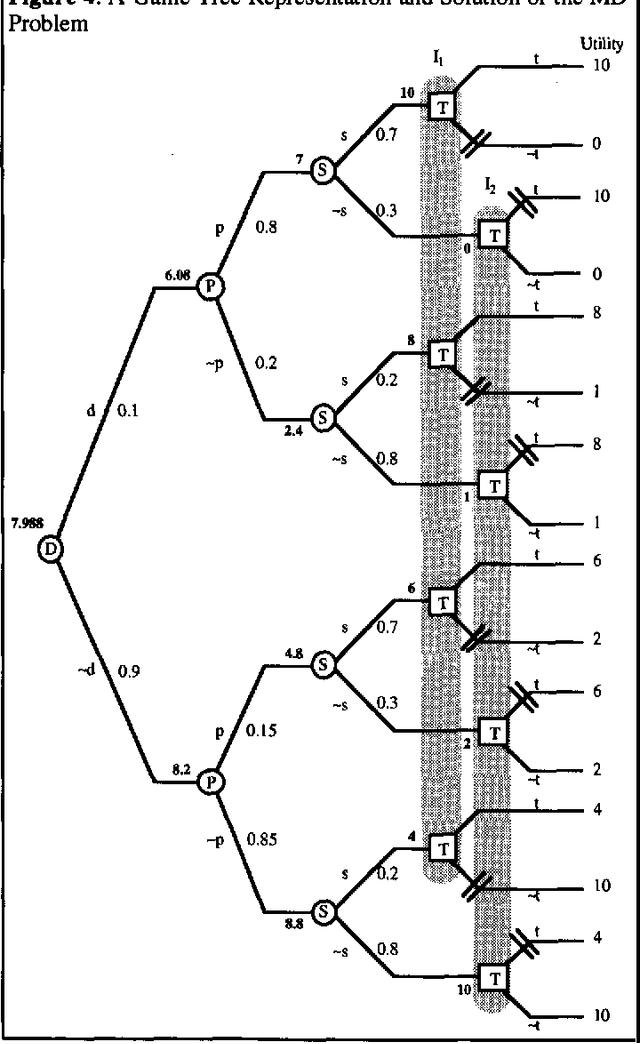
The main goal of this paper is to describe a new pruning method for solving decision trees and game trees. The pruning method for decision trees suggests a slight variant of decision trees that we call scenario trees. In scenario trees, we do not need a conditional probability for each edge emanating from a chance node. Instead, we require a joint probability for each path from the root node to a leaf node. We compare the pruning method to the traditional rollback method for decision trees and game trees. For problems that require Bayesian revision of probabilities, a scenario tree representation with the pruning method is more efficient than a decision tree representation with the rollback method. For game trees, the pruning method is more efficient than the rollback method.

Binary Join Trees

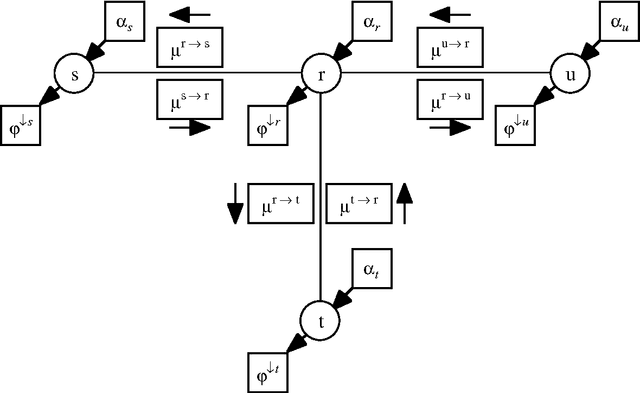
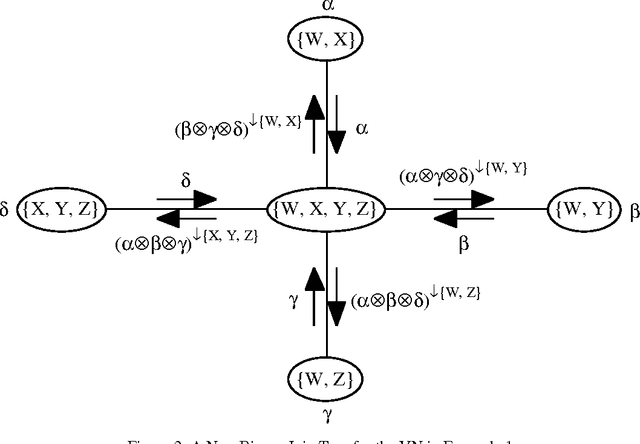
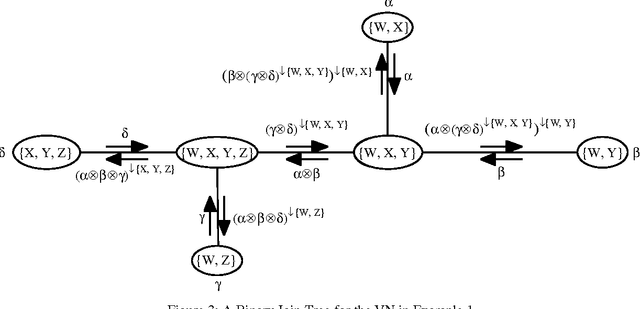
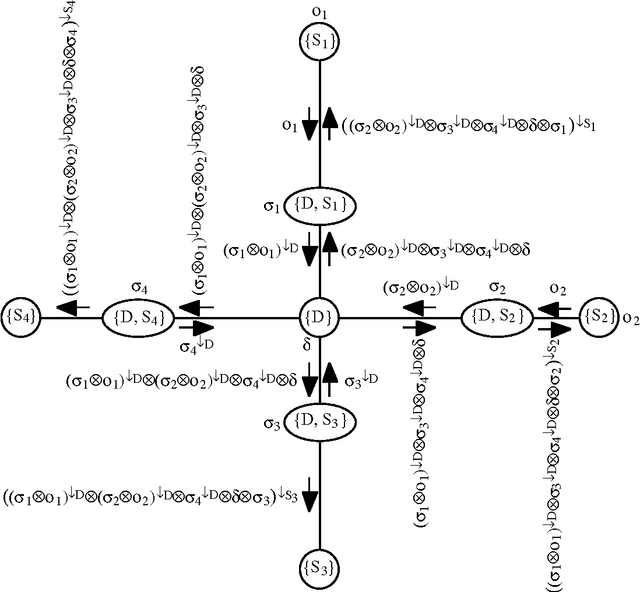
The main goal of this paper is to describe a data structure called binary join trees that are useful in computing multiple marginals efficiently using the Shenoy-Shafer architecture. We define binary join trees, describe their utility, and sketch a procedure for constructing them.