Probability Judgement in Artificial Intelligence

This paper is concerned with two theories of probability judgment: the Bayesian theory and the theory of belief functions. It illustrates these theories with some simple examples and discusses some of the issues that arise when we try to implement them in expert systems. The Bayesian theory is well known; its main ideas go back to the work of Thomas Bayes (1702-1761). The theory of belief functions, often called the Dempster-Shafer theory in the artificial intelligence community, is less well known, but it has even older antecedents; belief-function arguments appear in the work of George Hooper (16401723) and James Bernoulli (1654-1705). For elementary expositions of the theory of belief functions, see Shafer (1976, 1985).

Propagation of Belief Functions: A Distributed Approach

In this paper, we describe a scheme for propagating belief functions in certain kinds of trees using only local computations. This scheme generalizes the computational scheme proposed by Shafer and Logan1 for diagnostic trees of the type studied by Gordon and Shortliffe, and the slightly more general scheme given by Shafer for hierarchical evidence. It also generalizes the scheme proposed by Pearl for Bayesian causal trees (see Shenoy and Shafer). Pearl's causal trees and Gordon and Shortliffe's diagnostic trees are both ways of breaking the evidence that bears on a large problem down into smaller items of evidence that bear on smaller parts of the problem so that these smaller problems can be dealt with one at a time. This localization of effort is often essential in order to make the process of probability judgment feasible, both for the person who is making probability judgments and for the machine that is combining them. The basic structure for our scheme is a type of tree that generalizes both Pearl's and Gordon and Shortliffe's trees. Trees of this general type permit localized computation in Pearl's sense. They are based on qualitative judgments of conditional independence. We believe that the scheme we describe here will prove useful in expert systems. It is now clear that the successful propagation of probabilities or certainty factors in expert systems requires much more structure than can be provided in a pure production-system framework. Bayesian schemes, on the other hand, often make unrealistic demands for structure. The propagation of belief functions in trees and more general networks stands on a middle ground where some sensible and useful things can be done. We would like to emphasize that the basic idea of local computation for propagating probabilities is due to Judea Pearl. It is a very innovative idea; we do not believe that it can be found in the Bayesian literature prior to Pearl's work. We see our contribution as extending the usefulness of Pearl's idea by generalizing it from Bayesian probabilities to belief functions. In the next section, we give a brief introduction to belief functions. The notions of qualitative independence for partitions and a qualitative Markov tree are introduced in Section III. Finally, in Section IV, we describe a scheme for propagating belief functions in qualitative Markov trees.

Modifiable Combining Functions

Modifiable combining functions are a synthesis of two common approaches to combining evidence. They offer many of the advantages of these approaches and avoid some disadvantages. Because they facilitate the acquisition, representation, explanation, and modification of knowledge about combinations of evidence, they are proposed as a tool for knowledge engineers who build systems that reason under uncertainty, not as a normative theory of evidence.

An Axiomatic Framework for Bayesian and Belief-function Propagation

In this paper, we describe an abstract framework and axioms under which exact local computation of marginals is possible. The primitive objects of the framework are variables and valuations. The primitive operators of the framework are combination and marginalization. These operate on valuations. We state three axioms for these operators and we derive the possibility of local computation from the axioms. Next, we describe a propagation scheme for computing marginals of a valuation when we have a factorization of the valuation on a hypertree. Finally we show how the problem of computing marginals of joint probability distributions and joint belief functions fits the general framework.

Valuation-Based Systems for Discrete Optimization

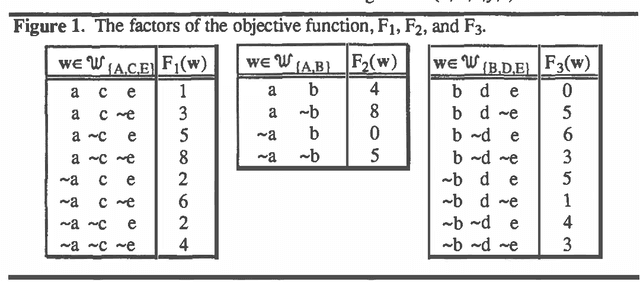
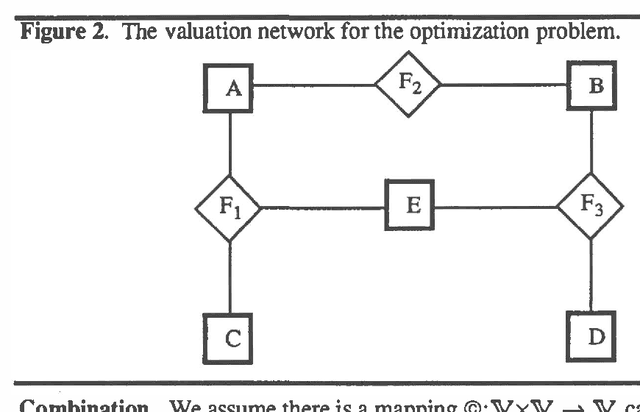
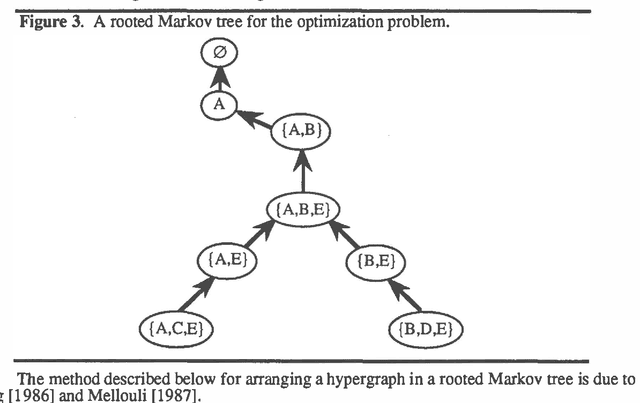
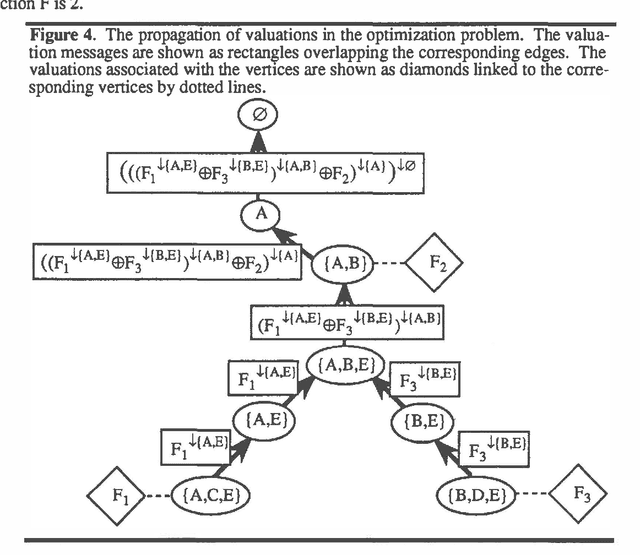
This paper describes valuation-based systems for representing and solving discrete optimization problems. In valuation-based systems, we represent information in an optimization problem using variables, sample spaces of variables, a set of values, and functions that map sample spaces of sets of variables to the set of values. The functions, called valuations, represent the factors of an objective function. Solving the optimization problem involves using two operations called combination and marginalization. Combination tells us how to combine the factors of the joint objective function. Marginalization is either maximization or minimization. Solving an optimization problem can be simply described as finding the marginal of the joint objective function for the empty set. We state some simple axioms that combination and marginalization need to satisfy to enable us to solve an optimization problem using local computation. For optimization problems, the solution method of valuation-based systems reduces to non-serial dynamic programming. Thus our solution method for VBS can be regarded as an abstract description of dynamic programming. And our axioms can be viewed as conditions that permit the use of dynamic programming.

A betting interpretation for probabilities and Dempster-Shafer degrees of belief

There are at least two ways to interpret numerical degrees of belief in terms of betting: (1) you can offer to bet at the odds defined by the degrees of belief, or (2) you can judge that a strategy for taking advantage of such betting offers will not multiply the capital it risks by a large factor. Both interpretations can be applied to ordinary additive probabilities and used to justify updating by conditioning. Only the second can be applied to Dempster-Shafer degrees of belief and used to justify Dempster's rule of combination.

A tutorial on conformal prediction

Conformal prediction uses past experience to determine precise levels of confidence in new predictions. Given an error probability $\epsilon$, together with a method that makes a prediction $\hat{y}$ of a label $y$, it produces a set of labels, typically containing $\hat{y}$, that also contains $y$ with probability $1-\epsilon$. Conformal prediction can be applied to any method for producing $\hat{y}$: a nearest-neighbor method, a support-vector machine, ridge regression, etc. Conformal prediction is designed for an on-line setting in which labels are predicted successively, each one being revealed before the next is predicted. The most novel and valuable feature of conformal prediction is that if the successive examples are sampled independently from the same distribution, then the successive predictions will be right $1-\epsilon$ of the time, even though they are based on an accumulating dataset rather than on independent datasets. In addition to the model under which successive examples are sampled independently, other on-line compression models can also use conformal prediction. The widely used Gaussian linear model is one of these. This tutorial presents a self-contained account of the theory of conformal prediction and works through several numerical examples. A more comprehensive treatment of the topic is provided in "Algorithmic Learning in a Random World", by Vladimir Vovk, Alex Gammerman, and Glenn Shafer (Springer, 2005).

Defensive forecasting for linear protocols

We consider a general class of forecasting protocols, called "linear protocols", and discuss several important special cases, including multi-class forecasting. Forecasting is formalized as a game between three players: Reality, whose role is to generate observations; Forecaster, whose goal is to predict the observations; and Skeptic, who tries to make money on any lack of agreement between Forecaster's predictions and the actual observations. Our main mathematical result is that for any continuous strategy for Skeptic in a linear protocol there exists a strategy for Forecaster that does not allow Skeptic's capital to grow. This result is a meta-theorem that allows one to transform any continuous law of probability in a linear protocol into a forecasting strategy whose predictions are guaranteed to satisfy this law. We apply this meta-theorem to a weak law of large numbers in Hilbert spaces to obtain a version of the K29 prediction algorithm for linear protocols and show that this version also satisfies the attractive properties of proper calibration and resolution under a suitable choice of its kernel parameter, with no assumptions about the way the data is generated.

Defensive forecasting

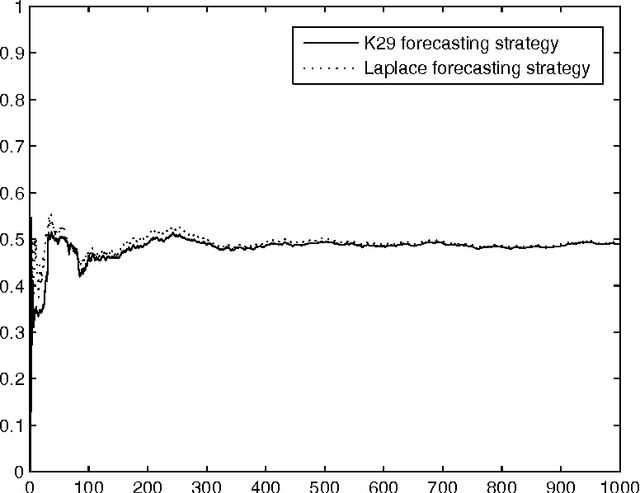
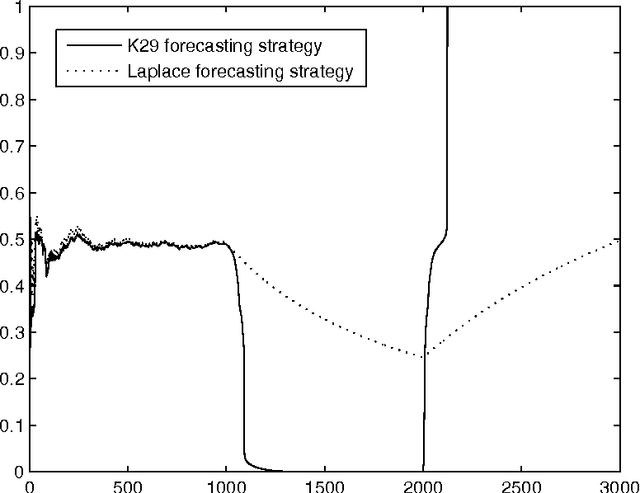
We consider how to make probability forecasts of binary labels. Our main mathematical result is that for any continuous gambling strategy used for detecting disagreement between the forecasts and the actual labels, there exists a forecasting strategy whose forecasts are ideal as far as this gambling strategy is concerned. A forecasting strategy obtained in this way from a gambling strategy demonstrating a strong law of large numbers is simplified and studied empirically.