Inductive randomness predictors

This paper introduces inductive randomness predictors, which form a superset of inductive conformal predictors. Its focus is on a very simple special case, binary inductive randomness predictors. It is interesting that binary inductive randomness predictors have an advantage over inductive conformal predictors, although they also have a serious disadvantage. This advantage will allow us to reach the surprising conclusion that non-trivial inductive conformal predictors are inadmissible in the sense of statistical decision theory.

Set and functional prediction: randomness, exchangeability, and conformal

This paper continues the study of the efficiency of conformal prediction as compared with more general randomness prediction and exchangeability prediction. It does not restrict itself to the case of classification, and our results will also be applicable to the case of regression. The price to pay is that efficiency will be attained only on average, albeit with respect to a wide range of probability measures on the label space.

Randomness, exchangeability, and conformal prediction

This note continues development of the functional theory of randomness, a modification of the algorithmic theory of randomness getting rid of unspecified additive constants. It introduces new kinds of confidence predictors, including randomness predictors (the most general confidence predictors based on the assumption of IID observations) and exchangeability predictors (the most general confidence predictors based on the assumption of exchangeable observations). The main result implies that both are close to conformal predictors and quantifies the difference between them.

Validity and efficiency of the conformal CUSUM procedure

In this paper we study the validity and efficiency of a conformal version of the CUSUM procedure for change detection both experimentally and theoretically.

Logic of subjective probability

In this paper I discuss both syntax and semantics of subjective probability. The semantics determines ways of testing probability statements. Among important varieties of subjective probabilities are intersubjective probabilities and impersonal probabilities, and I will argue that well-tested impersonal probabilities acquire features of objective probabilities. Jeffreys's law, my next topic, states that two successful probability forecasters must issue forecasts that are close to each other, thus supporting the idea of objective probabilities. Finally, I will discuss connections between subjective and frequentist probability.

Conformal testing: binary case with Markov alternatives

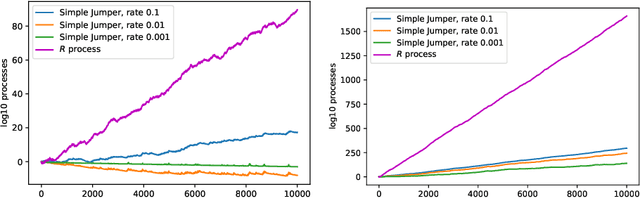
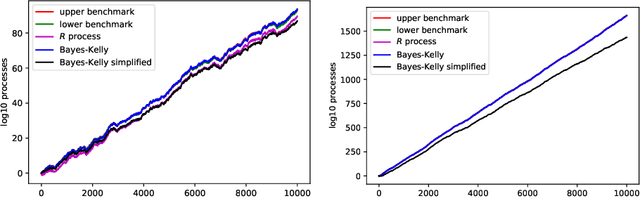
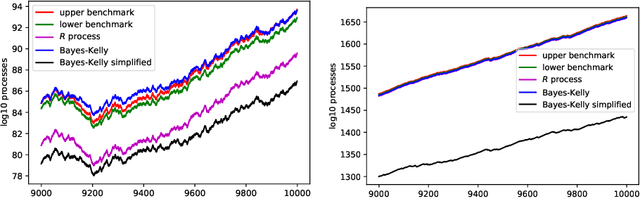
We continue study of conformal testing in binary model situations. In this note we consider Markov alternatives to the null hypothesis of exchangeability. We propose two new classes of conformal test martingales; one class is statistically efficient in our experiments, and the other class partially sacrifices statistical efficiency to gain computational efficiency.

Adaptive calibration for binary classification

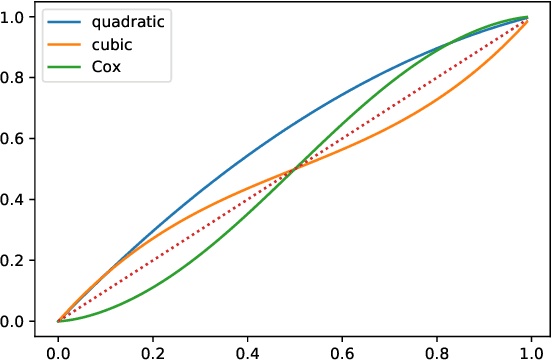
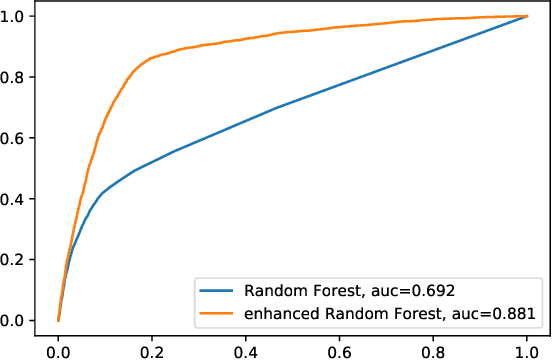
This note proposes a way of making probability forecasting rules less sensitive to changes in data distribution, concentrating on the simple case of binary classification. This is important in applications of machine learning, where the quality of a trained predictor may drop significantly in the process of its exploitation. Our techniques are based on recent work on conformal test martingales and older work on prediction with expert advice, namely tracking the best expert.

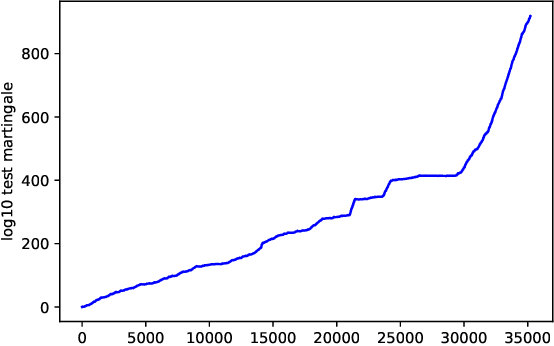
Enhancement of prediction algorithms by betting

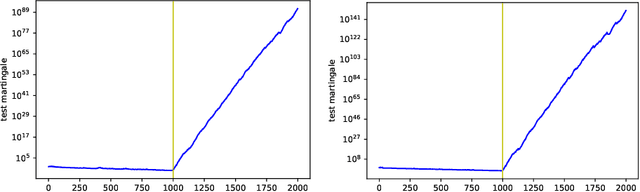
This note proposes a procedure for enhancing the quality of probabilistic prediction algorithms via betting against their predictions. It is inspired by the success of the conformal test martingales that have been developed recently.

Conformal testing in a binary model situation

Conformal testing is a way of testing the IID assumption based on conformal prediction. The topic of this note is computational evaluation of the performance of conformal testing in a model situation in which IID binary observations generated from a Bernoulli distribution are followed by IID binary observations generated from another Bernoulli distribution, with the parameters of the distributions and changepoint unknown. Existing conformal test martingales can be used for this task and work well in simple cases, but their efficiency can be improved greatly.

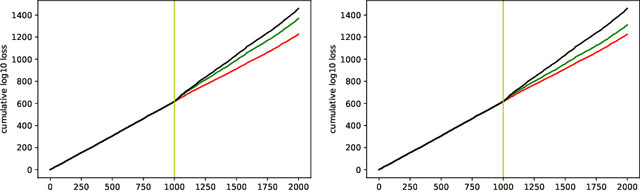
Retrain or not retrain: Conformal test martingales for change-point detection

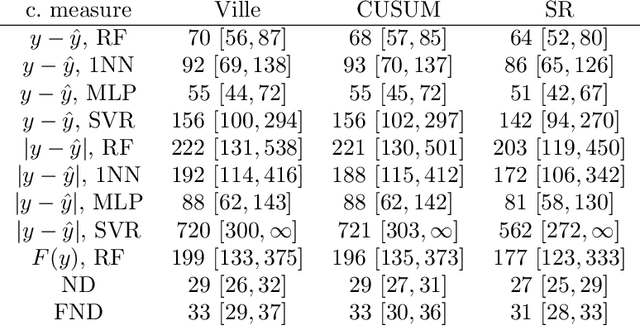
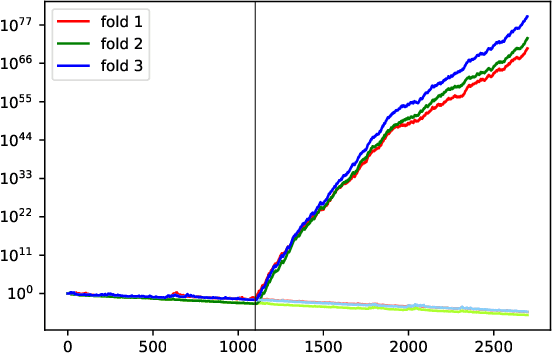
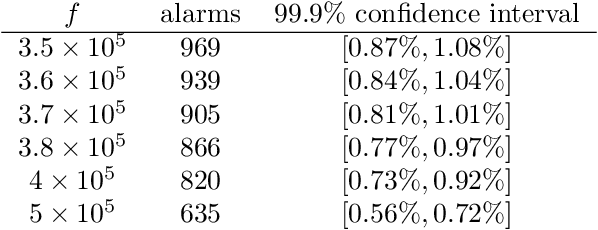
We argue for supplementing the process of training a prediction algorithm by setting up a scheme for detecting the moment when the distribution of the data changes and the algorithm needs to be retrained. Our proposed schemes are based on exchangeability martingales, i.e., processes that are martingales under any exchangeable distribution for the data. Our method, based on conformal prediction, is general and can be applied on top of any modern prediction algorithm. Its validity is guaranteed, and in this paper we make first steps in exploring its efficiency.