Validity and efficiency of the conformal CUSUM procedure

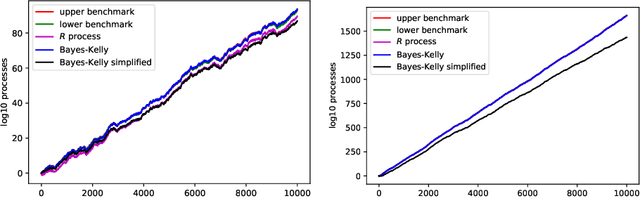
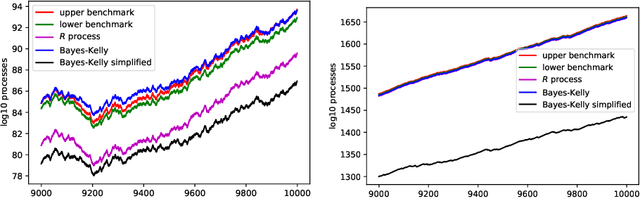
In this paper we study the validity and efficiency of a conformal version of the CUSUM procedure for change detection both experimentally and theoretically.

Conformal testing: binary case with Markov alternatives

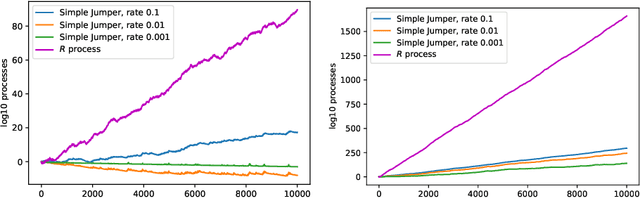
We continue study of conformal testing in binary model situations. In this note we consider Markov alternatives to the null hypothesis of exchangeability. We propose two new classes of conformal test martingales; one class is statistically efficient in our experiments, and the other class partially sacrifices statistical efficiency to gain computational efficiency.

Adaptive calibration for binary classification

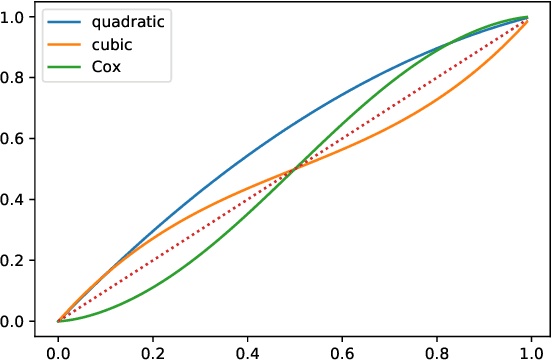
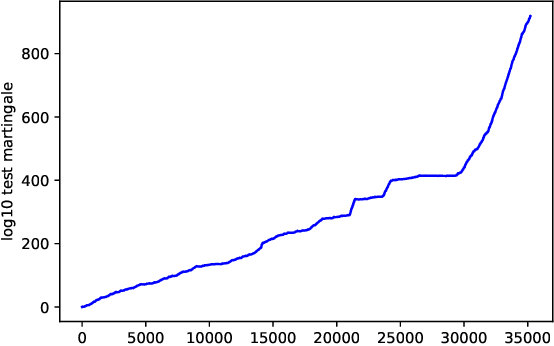
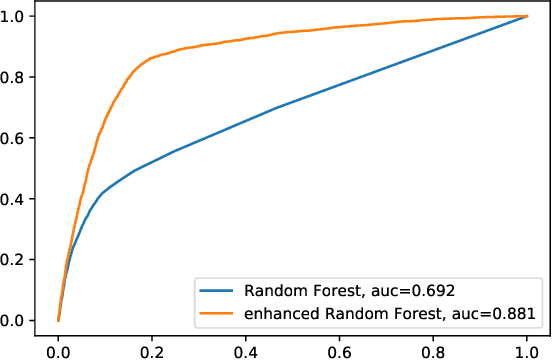
This note proposes a way of making probability forecasting rules less sensitive to changes in data distribution, concentrating on the simple case of binary classification. This is important in applications of machine learning, where the quality of a trained predictor may drop significantly in the process of its exploitation. Our techniques are based on recent work on conformal test martingales and older work on prediction with expert advice, namely tracking the best expert.

Retrain or not retrain: Conformal test martingales for change-point detection

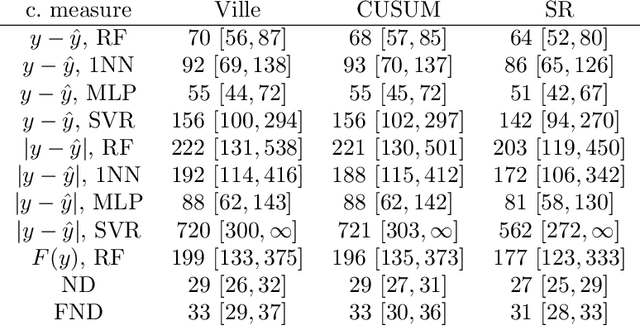
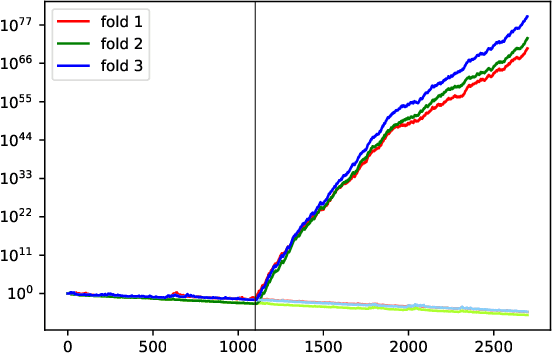
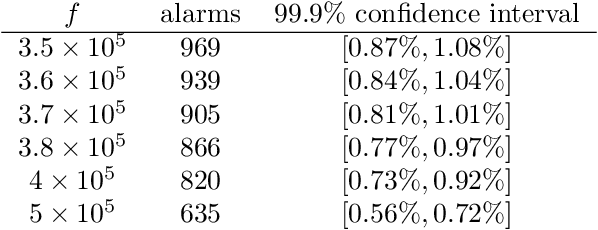
We argue for supplementing the process of training a prediction algorithm by setting up a scheme for detecting the moment when the distribution of the data changes and the algorithm needs to be retrained. Our proposed schemes are based on exchangeability martingales, i.e., processes that are martingales under any exchangeable distribution for the data. Our method, based on conformal prediction, is general and can be applied on top of any modern prediction algorithm. Its validity is guaranteed, and in this paper we make first steps in exploring its efficiency.

Computationally efficient versions of conformal predictive distributions

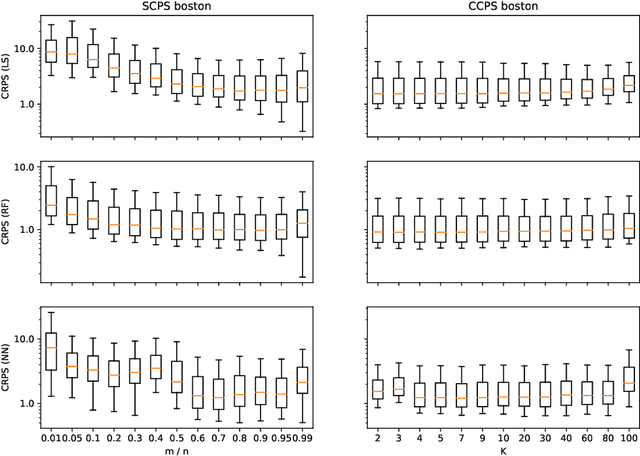
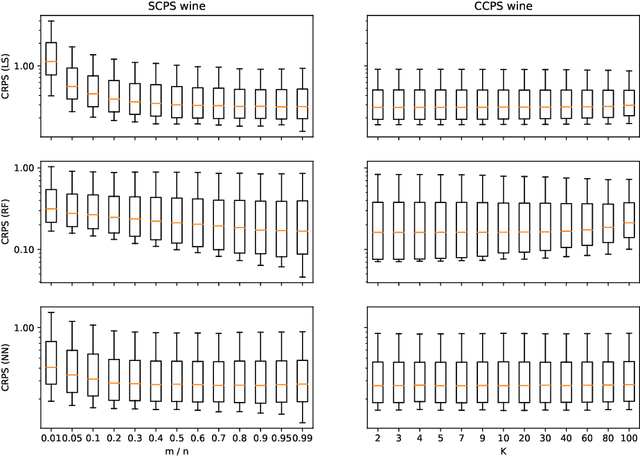
Conformal predictive systems are a recent modification of conformal predictors that output, in regression problems, probability distributions for labels of test observations rather than set predictions. The extra information provided by conformal predictive systems may be useful, e.g., in decision making problems. Conformal predictive systems inherit the relative computational inefficiency of conformal predictors. In this paper we discuss two computationally efficient versions of conformal predictive systems, which we call split conformal predictive systems and cross-conformal predictive systems. The main advantage of split conformal predictive systems is their guaranteed validity, whereas for cross-conformal predictive systems validity only holds empirically and in the absence of excessive randomization. The main advantage of cross-conformal predictive systems is their greater predictive efficiency.

Conformal calibrators

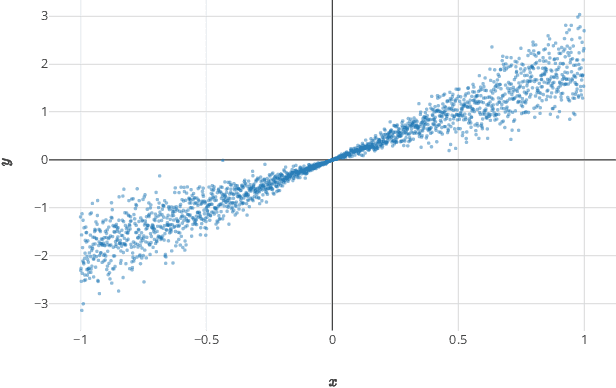
Most existing examples of full conformal predictive systems, split-conformal predictive systems, and cross-conformal predictive systems impose severe restrictions on the adaptation of predictive distributions to the test object at hand. In this paper we develop split-conformal and cross-conformal predictive systems that are fully adaptive. Our method consists in calibrating existing predictive systems; the input predictive system is not supposed to satisfy any properties of validity, whereas the output predictive system is guaranteed to be calibrated in probability. It is interesting that the method may also work without the IID assumption, standard in conformal prediction.

Conformal predictive distributions with kernels

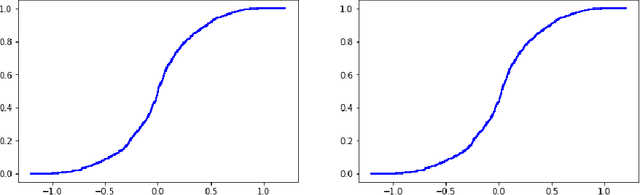
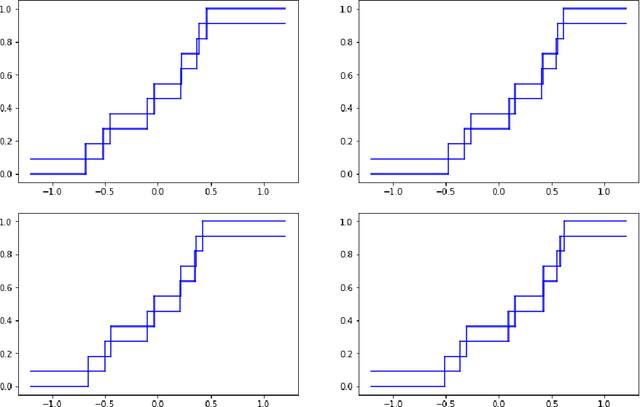
This paper reviews the checkered history of predictive distributions in statistics and discusses two developments, one from recent literature and the other new. The first development is bringing predictive distributions into machine learning, whose early development was so deeply influenced by two remarkable groups at the Institute of Automation and Remote Control. The second development is combining predictive distributions with kernel methods, which were originated by one of those groups, including Emmanuel Braverman.

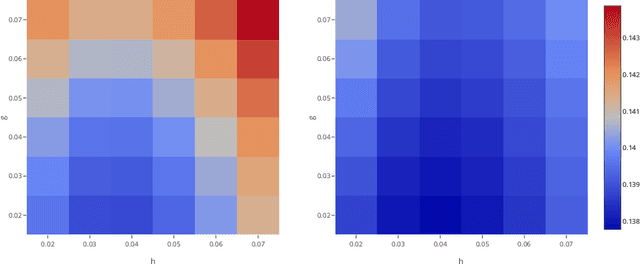
Criteria of efficiency for conformal prediction

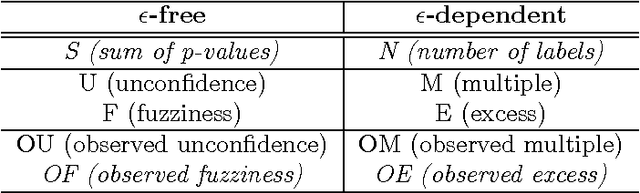
We study optimal conformity measures for various criteria of efficiency of classification in an idealised setting. This leads to an important class of criteria of efficiency that we call probabilistic; it turns out that the most standard criteria of efficiency used in literature on conformal prediction are not probabilistic unless the problem of classification is binary. We consider both unconditional and label-conditional conformal prediction.

Regression Conformal Prediction with Nearest Neighbours

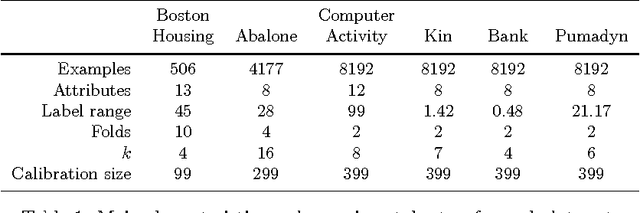
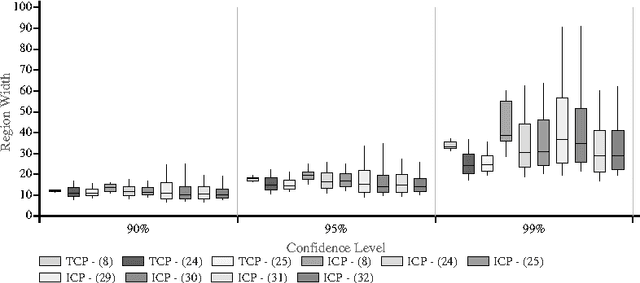
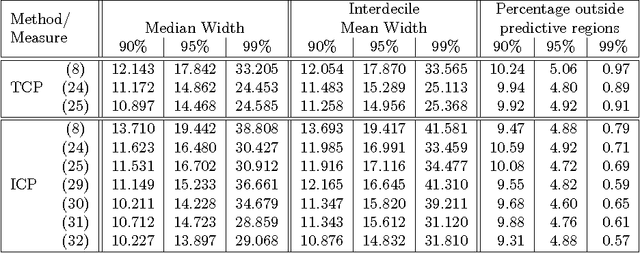
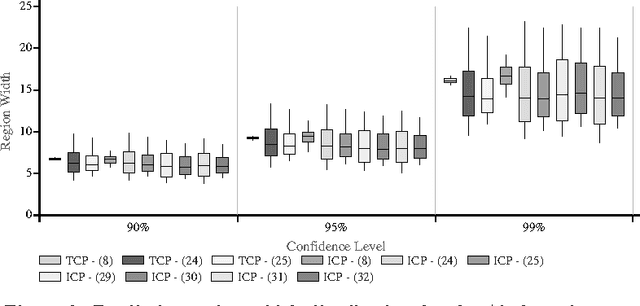
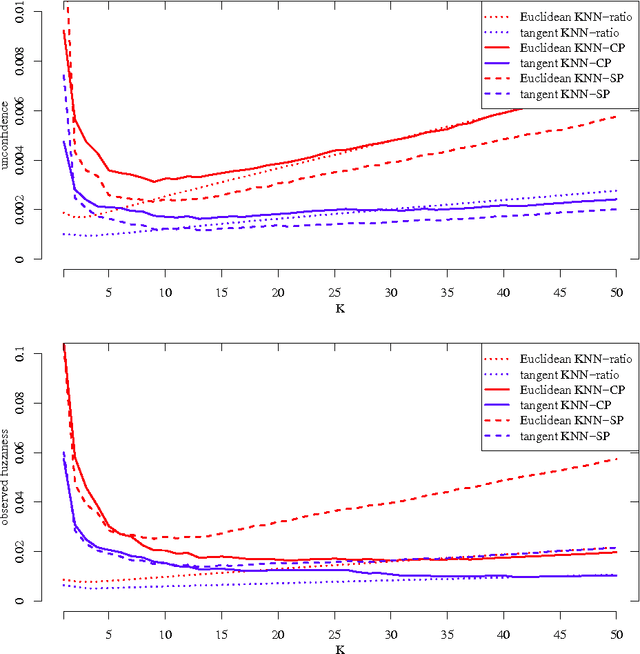
In this paper we apply Conformal Prediction (CP) to the k-Nearest Neighbours Regression (k-NNR) algorithm and propose ways of extending the typical nonconformity measure used for regression so far. Unlike traditional regression methods which produce point predictions, Conformal Predictors output predictive regions that satisfy a given confidence level. The regions produced by any Conformal Predictor are automatically valid, however their tightness and therefore usefulness depends on the nonconformity measure used by each CP. In effect a nonconformity measure evaluates how strange a given example is compared to a set of other examples based on some traditional machine learning algorithm. We define six novel nonconformity measures based on the k-Nearest Neighbours Regression algorithm and develop the corresponding CPs following both the original (transductive) and the inductive CP approaches. A comparison of the predictive regions produced by our measures with those of the typical regression measure suggests that a major improvement in terms of predictive region tightness is achieved by the new measures.

Learning by Transduction

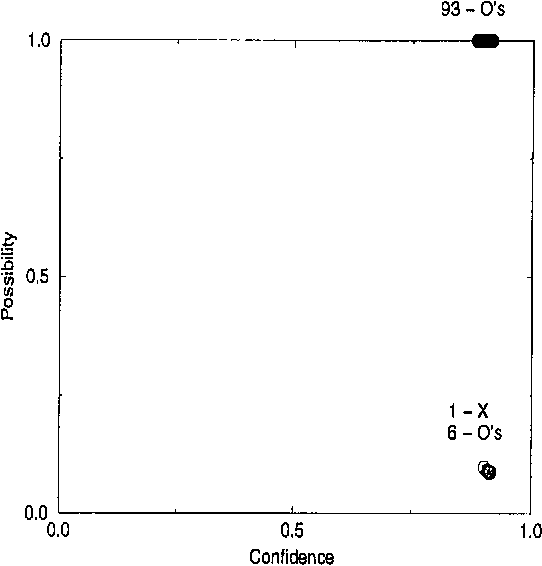
We describe a method for predicting a classification of an object given classifications of the objects in the training set, assuming that the pairs object/classification are generated by an i.i.d. process from a continuous probability distribution. Our method is a modification of Vapnik's support-vector machine; its main novelty is that it gives not only the prediction itself but also a practicable measure of the evidence found in support of that prediction. We also describe a procedure for assigning degrees of confidence to predictions made by the support vector machine. Some experimental results are presented, and possible extensions of the algorithms are discussed.