Computationally efficient versions of conformal predictive distributions

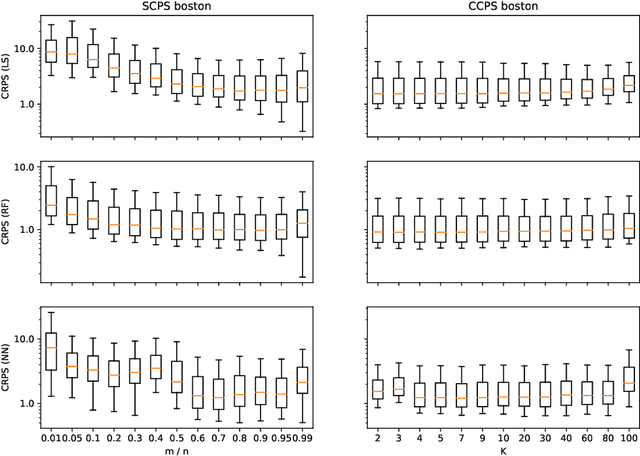
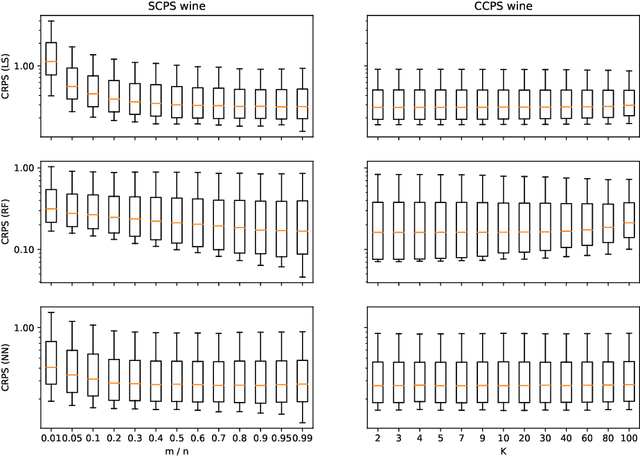
Conformal predictive systems are a recent modification of conformal predictors that output, in regression problems, probability distributions for labels of test observations rather than set predictions. The extra information provided by conformal predictive systems may be useful, e.g., in decision making problems. Conformal predictive systems inherit the relative computational inefficiency of conformal predictors. In this paper we discuss two computationally efficient versions of conformal predictive systems, which we call split conformal predictive systems and cross-conformal predictive systems. The main advantage of split conformal predictive systems is their guaranteed validity, whereas for cross-conformal predictive systems validity only holds empirically and in the absence of excessive randomization. The main advantage of cross-conformal predictive systems is their greater predictive efficiency.

Conformal predictive distributions with kernels

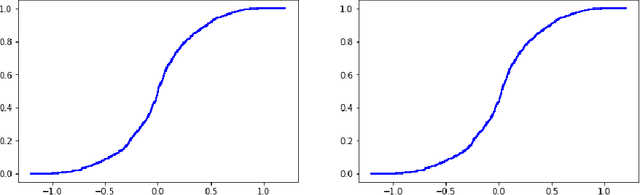
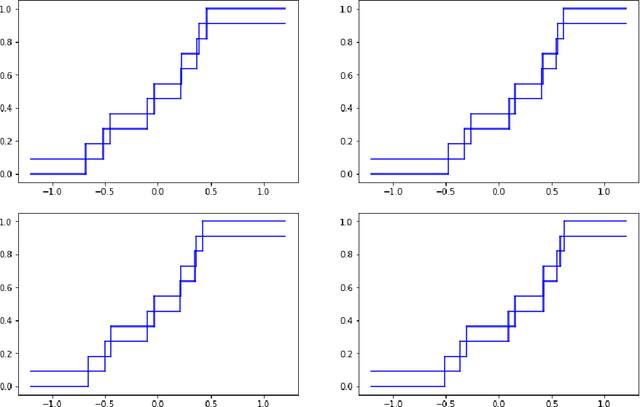
This paper reviews the checkered history of predictive distributions in statistics and discusses two developments, one from recent literature and the other new. The first development is bringing predictive distributions into machine learning, whose early development was so deeply influenced by two remarkable groups at the Institute of Automation and Remote Control. The second development is combining predictive distributions with kernel methods, which were originated by one of those groups, including Emmanuel Braverman.