Unifying distillation and privileged information

Distillation (Hinton et al., 2015) and privileged information (Vapnik & Izmailov, 2015) are two techniques that enable machines to learn from other machines. This paper unifies these two techniques into generalized distillation, a framework to learn from multiple machines and data representations. We provide theoretical and causal insight about the inner workings of generalized distillation, extend it to unsupervised, semisupervised and multitask learning scenarios, and illustrate its efficacy on a variety of numerical simulations on both synthetic and real-world data.

Constructive Setting of the Density Ratio Estimation Problem and its Rigorous Solution

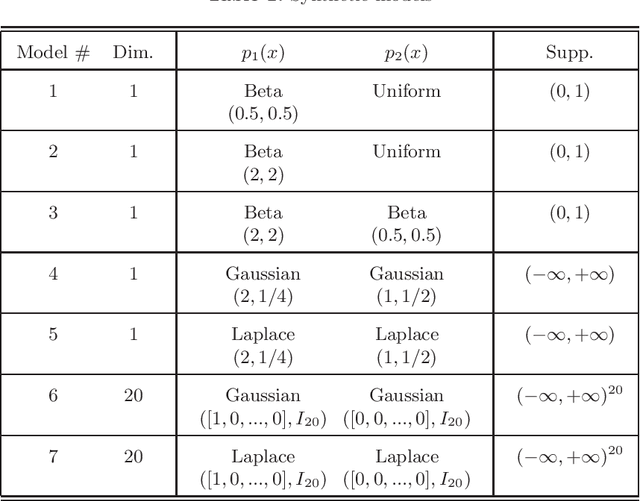
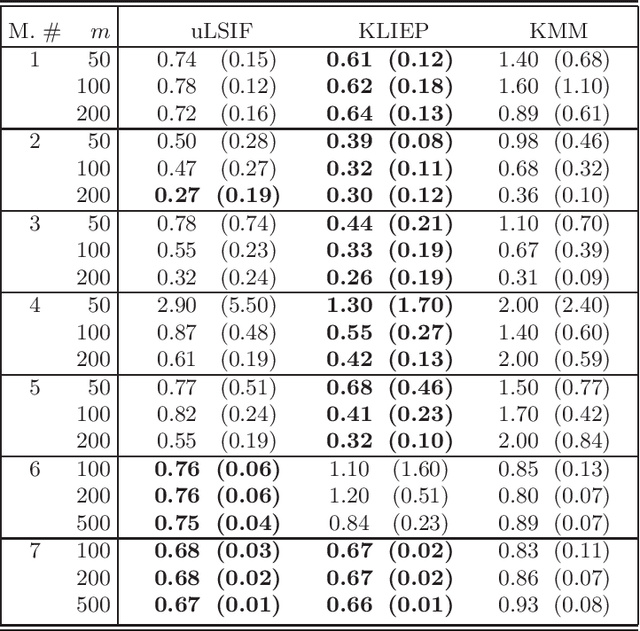
We introduce a general constructive setting of the density ratio estimation problem as a solution of a (multidimensional) integral equation. In this equation, not only its right hand side is known approximately, but also the integral operator is defined approximately. We show that this ill-posed problem has a rigorous solution and obtain the solution in a closed form. The key element of this solution is the novel V-matrix, which captures the geometry of the observed samples. We compare our method with three well-known previously proposed ones. Our experimental results demonstrate the good potential of the new approach.

Learning by Transduction

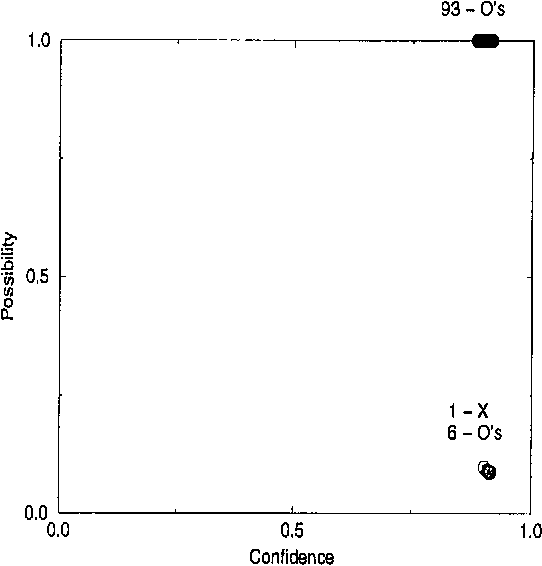
We describe a method for predicting a classification of an object given classifications of the objects in the training set, assuming that the pairs object/classification are generated by an i.i.d. process from a continuous probability distribution. Our method is a modification of Vapnik's support-vector machine; its main novelty is that it gives not only the prediction itself but also a practicable measure of the evidence found in support of that prediction. We also describe a procedure for assigning degrees of confidence to predictions made by the support vector machine. Some experimental results are presented, and possible extensions of the algorithms are discussed.