Defensive forecasting for linear protocols

We consider a general class of forecasting protocols, called "linear protocols", and discuss several important special cases, including multi-class forecasting. Forecasting is formalized as a game between three players: Reality, whose role is to generate observations; Forecaster, whose goal is to predict the observations; and Skeptic, who tries to make money on any lack of agreement between Forecaster's predictions and the actual observations. Our main mathematical result is that for any continuous strategy for Skeptic in a linear protocol there exists a strategy for Forecaster that does not allow Skeptic's capital to grow. This result is a meta-theorem that allows one to transform any continuous law of probability in a linear protocol into a forecasting strategy whose predictions are guaranteed to satisfy this law. We apply this meta-theorem to a weak law of large numbers in Hilbert spaces to obtain a version of the K29 prediction algorithm for linear protocols and show that this version also satisfies the attractive properties of proper calibration and resolution under a suitable choice of its kernel parameter, with no assumptions about the way the data is generated.

Defensive forecasting

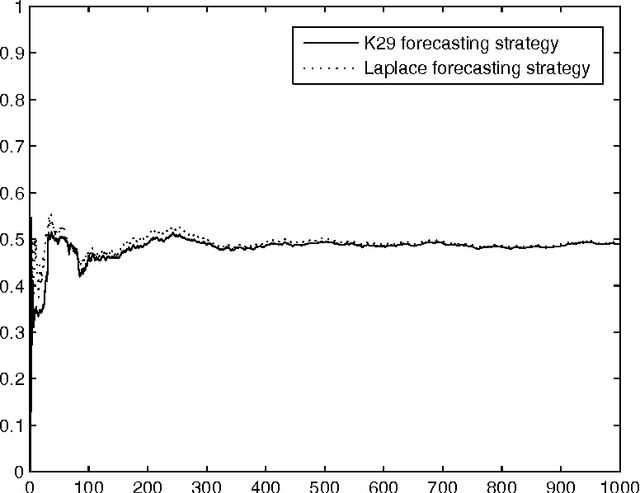
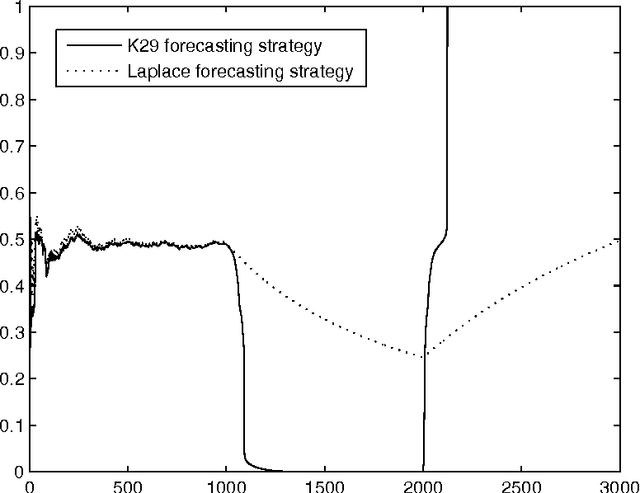
We consider how to make probability forecasts of binary labels. Our main mathematical result is that for any continuous gambling strategy used for detecting disagreement between the forecasts and the actual labels, there exists a forecasting strategy whose forecasts are ideal as far as this gambling strategy is concerned. A forecasting strategy obtained in this way from a gambling strategy demonstrating a strong law of large numbers is simplified and studied empirically.