Efficient and Scalable Bayesian Neural Nets with Rank-1 Factors

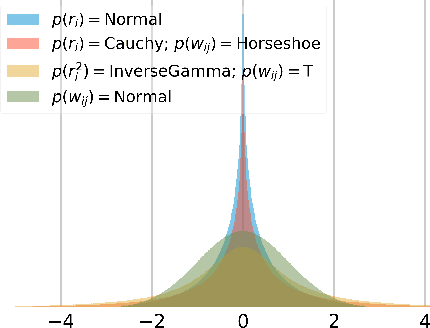
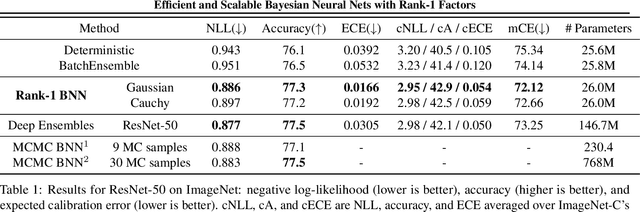
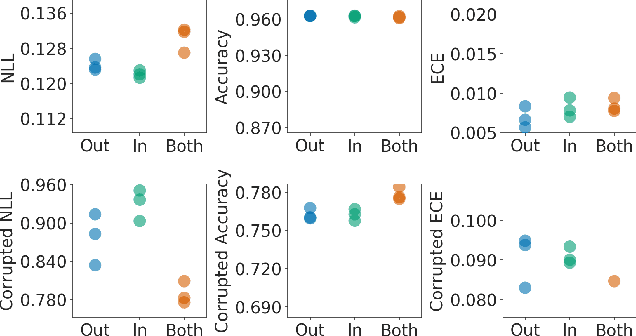
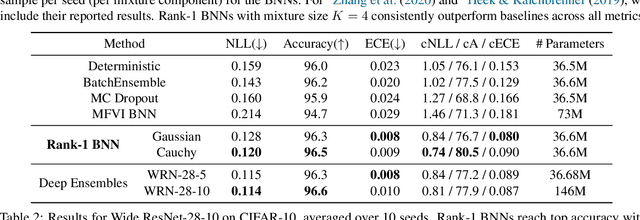
Bayesian neural networks (BNNs) demonstrate promising success in improving the robustness and uncertainty quantification of modern deep learning. However, they generally struggle with underfitting at scale and parameter efficiency. On the other hand, deep ensembles have emerged as alternatives for uncertainty quantification that, while outperforming BNNs on certain problems, also suffer from efficiency issues. It remains unclear how to combine the strengths of these two approaches and remediate their common issues. To tackle this challenge, we propose a rank-1 parameterization of BNNs, where each weight matrix involves only a distribution on a rank-1 subspace. We also revisit the use of mixture approximate posteriors to capture multiple modes, where unlike typical mixtures, this approach admits a significantly smaller memory increase (e.g., only a 0.4% increase for a ResNet-50 mixture of size 10). We perform a systematic empirical study on the choices of prior, variational posterior, and methods to improve training. For ResNet-50 on ImageNet, Wide ResNet 28-10 on CIFAR-10/100, and an RNN on MIMIC-III, rank-1 BNNs achieve state-of-the-art performance across log-likelihood, accuracy, and calibration on the test sets and out-of-distribution variants.

On Thompson Sampling with Langevin Algorithms

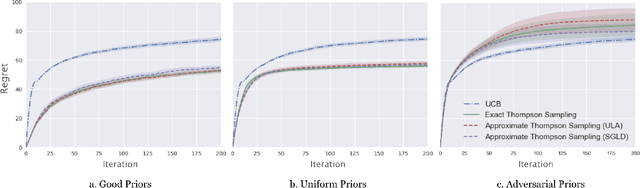
Thompson sampling is a methodology for multi-armed bandit problems that is known to enjoy favorable performance in both theory and practice. It does, however, have a significant limitation computationally, arising from the need for samples from posterior distributions at every iteration. We propose two Markov Chain Monte Carlo (MCMC) methods tailored to Thompson sampling to address this issue. We construct quickly converging Langevin algorithms to generate approximate samples that have accuracy guarantees, and we leverage novel posterior concentration rates to analyze the regret of the resulting approximate Thompson sampling algorithm. Further, we specify the necessary hyper-parameters for the MCMC procedure to guarantee optimal instance-dependent frequentist regret while having low computational complexity. In particular, our algorithms take advantage of both posterior concentration and a sample reuse mechanism to ensure that only a constant number of iterations and a constant amount of data is needed in each round. The resulting approximate Thompson sampling algorithm has logarithmic regret and its computational complexity does not scale with the time horizon of the algorithm.

Estimate exponential memory decay in Hidden Markov Model and its applications

Inference in hidden Markov model has been challenging in terms of scalability due to dependencies in the observation data. In this paper, we utilize the inherent memory decay in hidden Markov models, such that the forward and backward probabilities can be carried out with subsequences, enabling efficient inference over long sequences of observations. We formulate this forward filtering process in the setting of the random dynamical system and there exist Lyapunov exponents in the i.i.d random matrices production. And the rate of the memory decay is known as $\lambda_2-\lambda_1$, the gap of the top two Lyapunov exponents almost surely. An efficient and accurate algorithm is proposed to numerically estimate the gap after the soft-max parametrization. The length of subsequences $B$ given the controlled error $\epsilon$ is $B=\log(\epsilon)/(\lambda_2-\lambda_1)$. We theoretically prove the validity of the algorithm and demonstrate the effectiveness with numerical examples. The method developed here can be applied to widely used algorithms, such as mini-batch stochastic gradient method. Moreover, the continuity of Lyapunov spectrum ensures the estimated $B$ could be reused for the nearby parameter during the inference.