Efficient and Scalable Bayesian Neural Nets with Rank-1 Factors
Paper and Code
May 14, 2020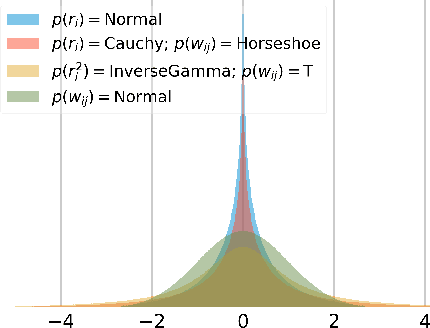
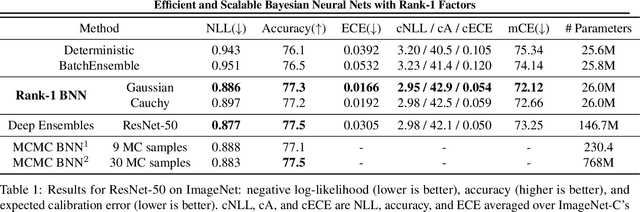
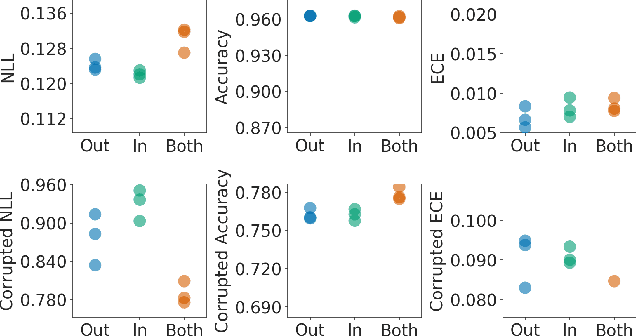
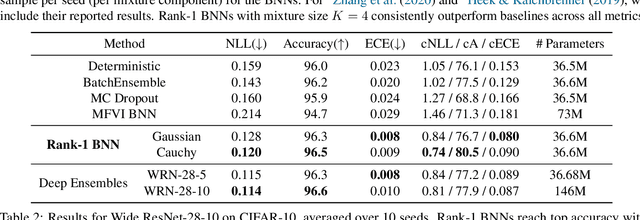
Bayesian neural networks (BNNs) demonstrate promising success in improving the robustness and uncertainty quantification of modern deep learning. However, they generally struggle with underfitting at scale and parameter efficiency. On the other hand, deep ensembles have emerged as alternatives for uncertainty quantification that, while outperforming BNNs on certain problems, also suffer from efficiency issues. It remains unclear how to combine the strengths of these two approaches and remediate their common issues. To tackle this challenge, we propose a rank-1 parameterization of BNNs, where each weight matrix involves only a distribution on a rank-1 subspace. We also revisit the use of mixture approximate posteriors to capture multiple modes, where unlike typical mixtures, this approach admits a significantly smaller memory increase (e.g., only a 0.4% increase for a ResNet-50 mixture of size 10). We perform a systematic empirical study on the choices of prior, variational posterior, and methods to improve training. For ResNet-50 on ImageNet, Wide ResNet 28-10 on CIFAR-10/100, and an RNN on MIMIC-III, rank-1 BNNs achieve state-of-the-art performance across log-likelihood, accuracy, and calibration on the test sets and out-of-distribution variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge