On Thompson Sampling with Langevin Algorithms

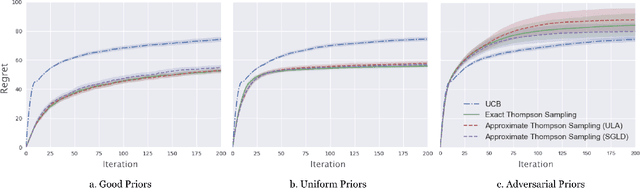
Thompson sampling is a methodology for multi-armed bandit problems that is known to enjoy favorable performance in both theory and practice. It does, however, have a significant limitation computationally, arising from the need for samples from posterior distributions at every iteration. We propose two Markov Chain Monte Carlo (MCMC) methods tailored to Thompson sampling to address this issue. We construct quickly converging Langevin algorithms to generate approximate samples that have accuracy guarantees, and we leverage novel posterior concentration rates to analyze the regret of the resulting approximate Thompson sampling algorithm. Further, we specify the necessary hyper-parameters for the MCMC procedure to guarantee optimal instance-dependent frequentist regret while having low computational complexity. In particular, our algorithms take advantage of both posterior concentration and a sample reuse mechanism to ensure that only a constant number of iterations and a constant amount of data is needed in each round. The resulting approximate Thompson sampling algorithm has logarithmic regret and its computational complexity does not scale with the time horizon of the algorithm.