Yanfang Wang
Exploring Lottery Ticket Hypothesis in Media Recommender Systems
Aug 02, 2021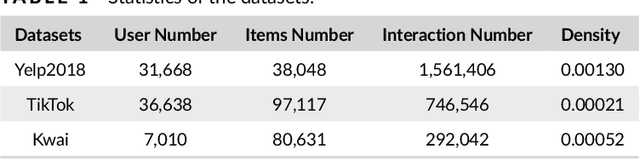
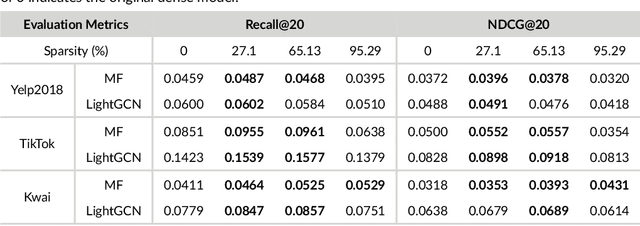
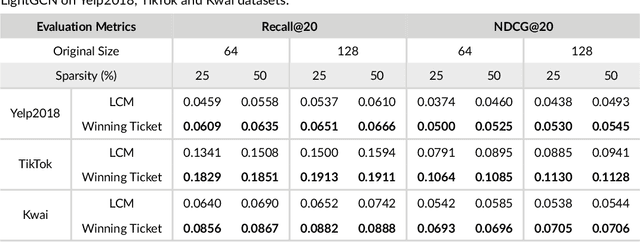
Abstract:Media recommender systems aim to capture users' preferences and provide precise personalized recommendation of media content. There are two critical components in the common paradigm of modern recommender models: (1) representation learning, which generates an embedding for each user and item; and (2) interaction modeling, which fits user preferences towards items based on their representations. Despite of great success, when a great amount of users and items exist, it usually needs to create, store, and optimize a huge embedding table, where the scale of model parameters easily reach millions or even larger. Hence, it naturally raises questions about the heavy recommender models: Do we really need such large-scale parameters? We get inspirations from the recently proposed lottery ticket hypothesis (LTH), which argues that the dense and over-parameterized model contains a much smaller and sparser sub-model that can reach comparable performance to the full model. In this paper, we extend LTH to media recommender systems, aiming to find the winning tickets in deep recommender models. To the best of our knowledge, this is the first work to study LTH in media recommender systems. With MF and LightGCN as the backbone models, we found that there widely exist winning tickets in recommender models. On three media convergence datasets -- Yelp2018, TikTok and Kwai, the winning tickets can achieve comparable recommendation performance with only 29%~48%, 7%~10% and 3%~17% of parameters, respectively.
From Dark Matter to Galaxies with Convolutional Neural Networks
Oct 17, 2019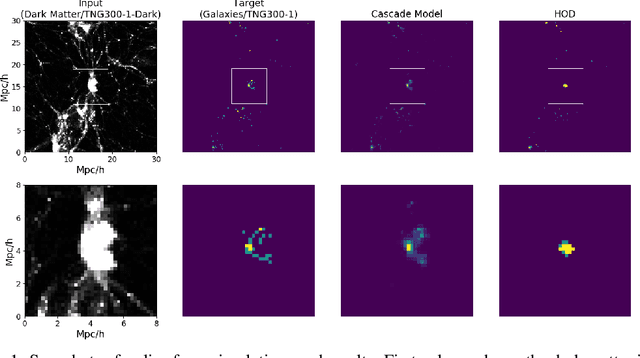
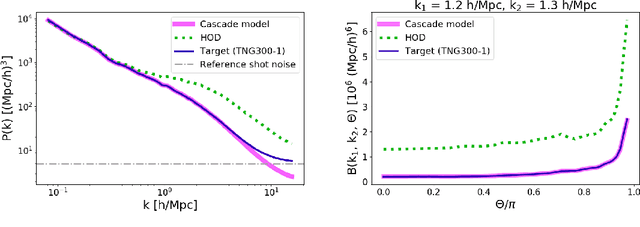
Abstract:Cosmological simulations play an important role in the interpretation of astronomical data, in particular in comparing observed data to our theoretical expectations. However, to compare data with these simulations, the simulations in principle need to include gravity, magneto-hydrodyanmics, radiative transfer, etc. These ideal large-volume simulations (gravo-magneto-hydrodynamical) are incredibly computationally expensive which can cost tens of millions of CPU hours to run. In this paper, we propose a deep learning approach to map from the dark-matter-only simulation (computationally cheaper) to the galaxy distribution (from the much costlier cosmological simulation). The main challenge of this task is the high sparsity in the target galaxy distribution: space is mainly empty. We propose a cascade architecture composed of a classification filter followed by a regression procedure. We show that our result outperforms a state-of-the-art model used in the astronomical community, and provides a good trade-off between computational cost and prediction accuracy.
From Dark Matter to Galaxies with Convolutional Networks
Apr 01, 2019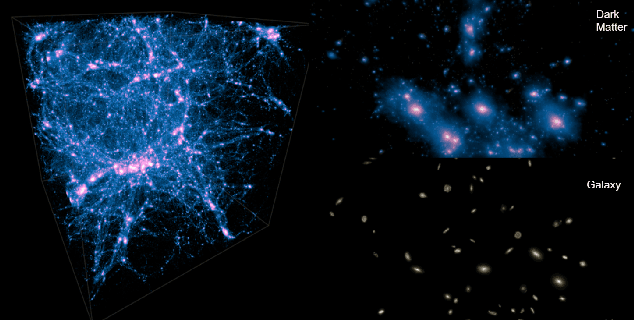
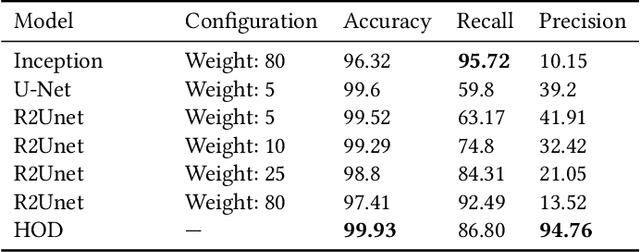
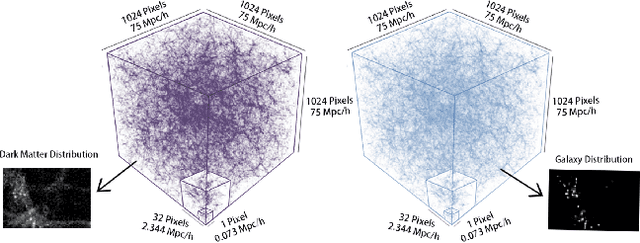
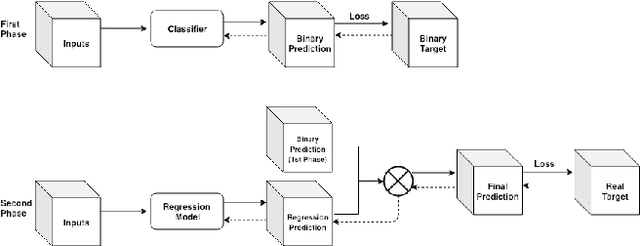
Abstract:Cosmological surveys aim at answering fundamental questions about our Universe, including the nature of dark matter or the reason of unexpected accelerated expansion of the Universe. In order to answer these questions, two important ingredients are needed: 1) data from observations and 2) a theoretical model that allows fast comparison between observation and theory. Most of the cosmological surveys observe galaxies, which are very difficult to model theoretically due to the complicated physics involved in their formation and evolution; modeling realistic galaxies over cosmological volumes requires running computationally expensive hydrodynamic simulations that can cost millions of CPU hours. In this paper, we propose to use deep learning to establish a mapping between the 3D galaxy distribution in hydrodynamic simulations and its underlying dark matter distribution. One of the major challenges in this pursuit is the very high sparsity in the predicted galaxy distribution. To this end, we develop a two-phase convolutional neural network architecture to generate fast galaxy catalogues, and compare our results against a standard cosmological technique. We find that our proposed approach either outperforms or is competitive with traditional cosmological techniques. Compared to the common methods used in cosmology, our approach also provides a nice trade-off between time-consumption (comparable to fastest benchmark in the literature) and the quality and accuracy of the predicted simulation. In combination with current and upcoming data from cosmological observations, our method has the potential to answer fundamental questions about our Universe with the highest accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge