Speed-enhanced Subdomain Adaptation Regression for Long-term Stable Neural Decoding in Brain-computer Interfaces

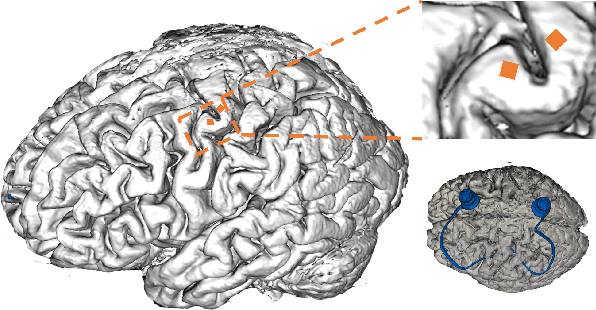
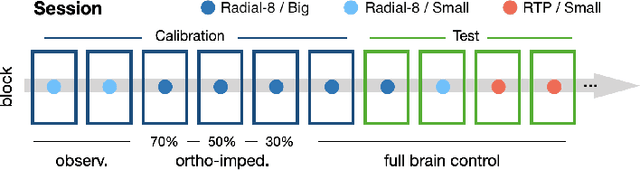
Brain-computer interfaces (BCIs) offer a means to convert neural signals into control signals, providing a potential restoration of movement for people with paralysis. Despite their promise, BCIs face a significant challenge in maintaining decoding accuracy over time due to neural nonstationarities. However, the decoding accuracy of BCI drops severely across days due to the neural data drift. While current recalibration techniques address this issue to a degree, they often fail to leverage the limited labeled data, to consider the signal correlation between two days, or to perform conditional alignment in regression tasks. This paper introduces a novel approach to enhance recalibration performance. We begin with preliminary experiments that reveal the temporal patterns of neural signal changes and identify three critical elements for effective recalibration: global alignment, conditional speed alignment, and feature-label consistency. Building on these insights, we propose the Speed-enhanced Subdomain Adaptation Regression (SSAR) framework, integrating semi-supervised learning with domain adaptation techniques in regression neural decoding. SSAR employs Speed-enhanced Subdomain Alignment (SeSA) for global and speed conditional alignment of similarly labeled data, with Contrastive Consistency Constraint (CCC) to enhance the alignment of SeSA by reinforcing feature-label consistency through contrastive learning. Our comprehensive set of experiments, both qualitative and quantitative, substantiate the superior recalibration performance and robustness of SSAR.

Tensor Recovery Based on A Novel Non-convex Function Minimax Logarithmic Concave Penalty Function

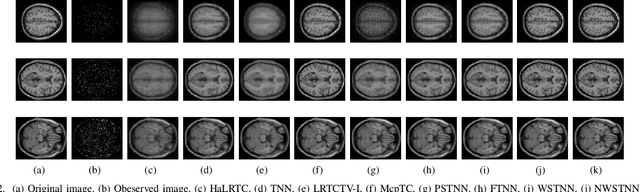
Non-convex relaxation methods have been widely used in tensor recovery problems, and compared with convex relaxation methods, can achieve better recovery results. In this paper, a new non-convex function, Minimax Logarithmic Concave Penalty (MLCP) function, is proposed, and some of its intrinsic properties are analyzed, among which it is interesting to find that the Logarithmic function is an upper bound of the MLCP function. The proposed function is generalized to tensor cases, yielding tensor MLCP and weighted tensor $L\gamma$-norm. Consider that its explicit solution cannot be obtained when applying it directly to the tensor recovery problem. Therefore, the corresponding equivalence theorems to solve such problem are given, namely, tensor equivalent MLCP theorem and equivalent weighted tensor $L\gamma$-norm theorem. In addition, we propose two EMLCP-based models for classic tensor recovery problems, namely low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA), and design proximal alternate linearization minimization (PALM) algorithms to solve them individually. Furthermore, based on the Kurdyka-{\L}ojasiwicz property, it is proved that the solution sequence of the proposed algorithm has finite length and converges to the critical point globally. Finally, Extensive experiments show that proposed algorithm achieve good results, and it is confirmed that the MLCP function is indeed better than the Logarithmic function in the minimization problem, which is consistent with the analysis of theoretical properties.

Dynamic Ensemble Bayesian Filter for Robust Control of a Human Brain-machine Interface

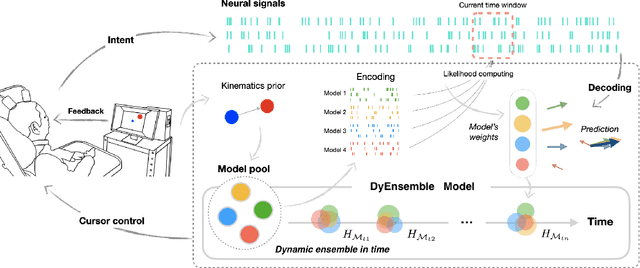
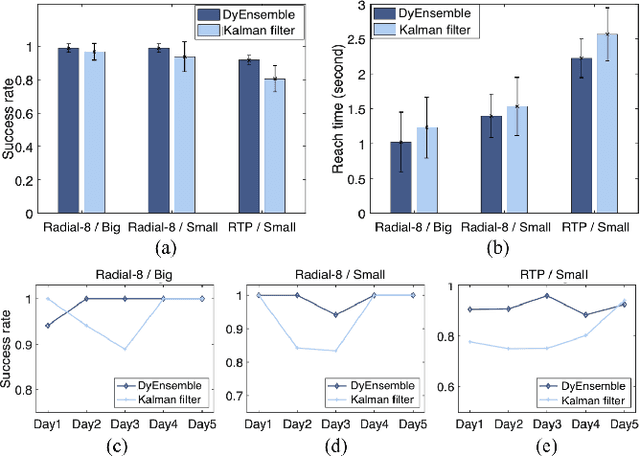
Objective: Brain-machine interfaces (BMIs) aim to provide direct brain control of devices such as prostheses and computer cursors, which have demonstrated great potential for mobility restoration. One major limitation of current BMIs lies in the unstable performance in online control due to the variability of neural signals, which seriously hinders the clinical availability of BMIs. Method: To deal with the neural variability in online BMI control, we propose a dynamic ensemble Bayesian filter (DyEnsemble). DyEnsemble extends Bayesian filters with a dynamic measurement model, which adjusts its parameters in time adaptively with neural changes. This is achieved by learning a pool of candidate functions and dynamically weighting and assembling them according to neural signals. In this way, DyEnsemble copes with variability in signals and improves the robustness of online control. Results: Online BMI experiments with a human participant demonstrate that, compared with the velocity Kalman filter, DyEnsemble significantly improves the control accuracy (increases the success rate by 13.9% and reduces the reach time by 13.5% in the random target pursuit task) and robustness (performs more stably over different experiment days). Conclusion: Our results demonstrate the superiority of DyEnsemble in online BMI control. Significance: DyEnsemble frames a novel and flexible framework for robust neural decoding, which is beneficial to different neural decoding applications.