Hongbing Zhang
Low-rank tensor completion via a novel minimax $p$-th order concave penalty function
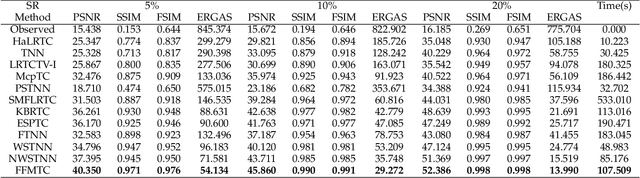
Feb 27, 2025Abstract:Low-rank tensor completion (LRTC) has attracted significant attention in fields such as computer vision and pattern recognition. Among the various techniques employed in LRTC, non-convex relaxation methods have been widely studied for their effectiveness in handling tensor singular values, which are crucial for accurate tensor recovery. However, the minimax concave penalty (MCP) function, a commonly used non-convex relaxation, exhibits a critical limitation: it effectively preserves large singular values but inadequately processes small ones. To address this issue, a novel minimax $p$-th order concave penalty (MPCP) function is proposed. Building on this advancement, a tensor $p$-th order $\tau$ norm is proposed as a non-convex relaxation for tensor rank estimation, thereby establishing an MPCP-based LRTC model. Furthermore, theoretical guarantees of convergence are provided for the proposed method. Experimental results on multiple real datasets demonstrate that the proposed method outperforms the state-of-the-art methods in both visual quality and quantitative metrics.
Nonconvex third-order Tensor Recovery Based on Logarithmic Minimax Function
Sep 28, 2023Abstract:Recent researches have shown that low-rank tensor recovery based non-convex relaxation has gained extensive attention. In this context, we propose a new Logarithmic Minimax (LM) function. The comparative analysis between the LM function and the Logarithmic, Minimax concave penalty (MCP), and Minimax Logarithmic concave penalty (MLCP) functions reveals that the proposed function can protect large singular values while imposing stronger penalization on small singular values. Based on this, we define a weighted tensor LM norm as a non-convex relaxation for tensor tubal rank. Subsequently, we propose the TLM-based low-rank tensor completion (LRTC) model and the TLM-based tensor robust principal component analysis (TRPCA) model respectively. Furthermore, we provide theoretical convergence guarantees for the proposed methods. Comprehensive experiments were conducted on various real datasets, and a comparison analysis was made with the similar EMLCP method. The results demonstrate that the proposed method outperforms the state-of-the-art methods.
Tensor Recovery Based on A Novel Non-convex Function Minimax Logarithmic Concave Penalty Function
Jun 25, 2022
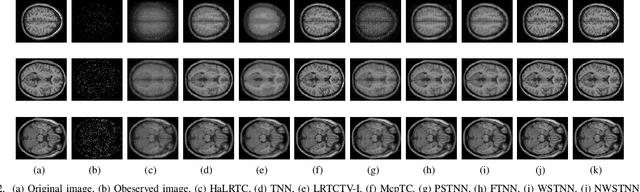


Abstract:Non-convex relaxation methods have been widely used in tensor recovery problems, and compared with convex relaxation methods, can achieve better recovery results. In this paper, a new non-convex function, Minimax Logarithmic Concave Penalty (MLCP) function, is proposed, and some of its intrinsic properties are analyzed, among which it is interesting to find that the Logarithmic function is an upper bound of the MLCP function. The proposed function is generalized to tensor cases, yielding tensor MLCP and weighted tensor $L\gamma$-norm. Consider that its explicit solution cannot be obtained when applying it directly to the tensor recovery problem. Therefore, the corresponding equivalence theorems to solve such problem are given, namely, tensor equivalent MLCP theorem and equivalent weighted tensor $L\gamma$-norm theorem. In addition, we propose two EMLCP-based models for classic tensor recovery problems, namely low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA), and design proximal alternate linearization minimization (PALM) algorithms to solve them individually. Furthermore, based on the Kurdyka-{\L}ojasiwicz property, it is proved that the solution sequence of the proposed algorithm has finite length and converges to the critical point globally. Finally, Extensive experiments show that proposed algorithm achieve good results, and it is confirmed that the MLCP function is indeed better than the Logarithmic function in the minimization problem, which is consistent with the analysis of theoretical properties.
Tensor Recovery Based on Tensor Equivalent Minimax-Concave Penalty
Jan 30, 2022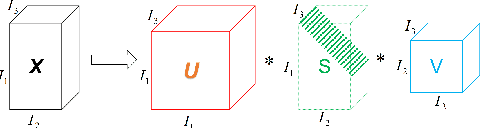

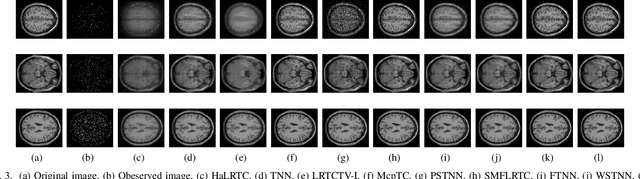

Abstract:Tensor recovery is an important problem in computer vision and machine learning. It usually uses the convex relaxation of tensor rank and $l_{0}$ norm, i.e., the nuclear norm and $l_{1}$ norm respectively, to solve the problem. It is well known that convex approximations produce biased estimators. In order to overcome this problem, a corresponding non-convex regularizer has been proposed to solve it. Inspired by matrix equivalent Minimax-Concave Penalty (EMCP), we propose and prove theorems of tensor equivalent Minimax-Concave Penalty (TEMCP). The tensor equivalent MCP (TEMCP) as a non-convex regularizer and the equivalent weighted tensor $\gamma$ norm (EWTGN) which can represent the low-rank part are obtained. Both of them can realize weight adaptive. At the same time, we propose two corresponding adaptive models for two classical tensor recovery problems, low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA), and the optimization algorithm is based on alternating direction multiplier (ADMM). This novel iterative adaptive algorithm can produce more accurate tensor recovery effect. For the tensor completion model, multispectral image (MSI), magnetic resonance imaging (MRI) and color video (CV) data sets are considered, while for the tensor robust principal component analysis model, hyperspectral image (HSI) denoising under gaussian noise plus salt and pepper noise is considered. The proposed algorithm is superior to the state-of-arts method, and the algorithm is guaranteed to meet the reduction and convergence through experiments.
Tensor Full Feature Measure and Its Nonconvex Relaxation Applications to Tensor Recovery
Sep 25, 2021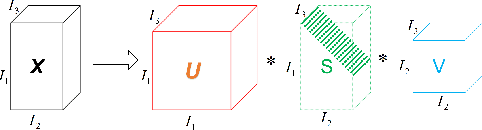


Abstract:Tensor sparse modeling as a promising approach, in the whole of science and engineering has been a huge success. As is known to all, various data in practical application are often generated by multiple factors, so the use of tensors to represent the data containing the internal structure of multiple factors came into being. However, different from the matrix case, constructing reasonable sparse measure of tensor is a relatively difficult and very important task. Therefore, in this paper, we propose a new tensor sparsity measure called Tensor Full Feature Measure (FFM). It can simultaneously describe the feature information of each dimension of the tensor and the related features between two dimensions, and connect the Tucker rank with the tensor tube rank. This measurement method can describe the sparse features of the tensor more comprehensively. On this basis, we establish its non-convex relaxation, and apply FFM to low rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). LRTC and TRPCA models based on FFM are proposed, and two efficient Alternating Direction Multiplier Method (ADMM) algorithms are developed to solve the proposed model. A variety of real numerical experiments substantiate the superiority of the proposed methods beyond state-of-the-arts.
Fast and Accurate Low-Rank Tensor Completion Methods Based on QR Decomposition and $L_{2,1}$ Norm Minimization
Aug 14, 2021



Abstract:More recently, an Approximate SVD Based on Qatar Riyal (QR) Decomposition (CSVD-QR) method for matrix complete problem is presented, whose computational complexity is $O(r^2(m+n))$, which is mainly due to that $r$ is far less than $\min\{m,n\}$, where $r$ represents the largest number of singular values of matrix $X$. What is particularly interesting is that after replacing the nuclear norm with the $L_{2,1}$ norm proposed based on this decomposition, as the upper bound of the nuclear norm, when the intermediate matrix $D$ in its decomposition is close to the diagonal matrix, it will converge to the nuclear norm, and is exactly equal, when the $D$ matrix is equal to the diagonal matrix, to the nuclear norm, which ingeniously avoids the calculation of the singular value of the matrix. To the best of our knowledge, there is no literature to generalize and apply it to solve tensor complete problems. Inspired by this, in this paper we propose a class of tensor minimization model based on $L_{2,1}$ norm and CSVD-QR method for the tensor complete problem, which is convex and therefore has a global minimum solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge