Tensor Recovery Based on Tensor Equivalent Minimax-Concave Penalty

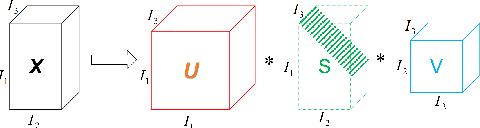
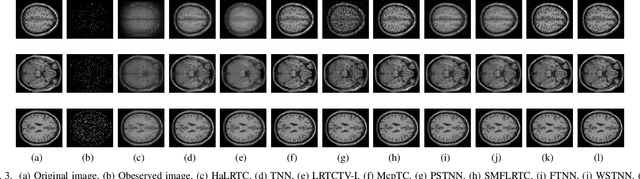
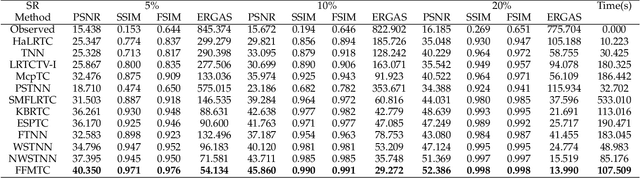
Tensor recovery is an important problem in computer vision and machine learning. It usually uses the convex relaxation of tensor rank and $l_{0}$ norm, i.e., the nuclear norm and $l_{1}$ norm respectively, to solve the problem. It is well known that convex approximations produce biased estimators. In order to overcome this problem, a corresponding non-convex regularizer has been proposed to solve it. Inspired by matrix equivalent Minimax-Concave Penalty (EMCP), we propose and prove theorems of tensor equivalent Minimax-Concave Penalty (TEMCP). The tensor equivalent MCP (TEMCP) as a non-convex regularizer and the equivalent weighted tensor $\gamma$ norm (EWTGN) which can represent the low-rank part are obtained. Both of them can realize weight adaptive. At the same time, we propose two corresponding adaptive models for two classical tensor recovery problems, low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA), and the optimization algorithm is based on alternating direction multiplier (ADMM). This novel iterative adaptive algorithm can produce more accurate tensor recovery effect. For the tensor completion model, multispectral image (MSI), magnetic resonance imaging (MRI) and color video (CV) data sets are considered, while for the tensor robust principal component analysis model, hyperspectral image (HSI) denoising under gaussian noise plus salt and pepper noise is considered. The proposed algorithm is superior to the state-of-arts method, and the algorithm is guaranteed to meet the reduction and convergence through experiments.

Tensor Full Feature Measure and Its Nonconvex Relaxation Applications to Tensor Recovery

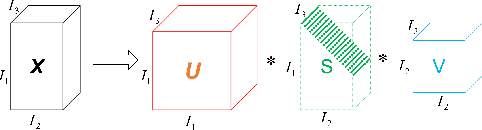
Tensor sparse modeling as a promising approach, in the whole of science and engineering has been a huge success. As is known to all, various data in practical application are often generated by multiple factors, so the use of tensors to represent the data containing the internal structure of multiple factors came into being. However, different from the matrix case, constructing reasonable sparse measure of tensor is a relatively difficult and very important task. Therefore, in this paper, we propose a new tensor sparsity measure called Tensor Full Feature Measure (FFM). It can simultaneously describe the feature information of each dimension of the tensor and the related features between two dimensions, and connect the Tucker rank with the tensor tube rank. This measurement method can describe the sparse features of the tensor more comprehensively. On this basis, we establish its non-convex relaxation, and apply FFM to low rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). LRTC and TRPCA models based on FFM are proposed, and two efficient Alternating Direction Multiplier Method (ADMM) algorithms are developed to solve the proposed model. A variety of real numerical experiments substantiate the superiority of the proposed methods beyond state-of-the-arts.

Fast and Accurate Low-Rank Tensor Completion Methods Based on QR Decomposition and $L_{2,1}$ Norm Minimization

More recently, an Approximate SVD Based on Qatar Riyal (QR) Decomposition (CSVD-QR) method for matrix complete problem is presented, whose computational complexity is $O(r^2(m+n))$, which is mainly due to that $r$ is far less than $\min\{m,n\}$, where $r$ represents the largest number of singular values of matrix $X$. What is particularly interesting is that after replacing the nuclear norm with the $L_{2,1}$ norm proposed based on this decomposition, as the upper bound of the nuclear norm, when the intermediate matrix $D$ in its decomposition is close to the diagonal matrix, it will converge to the nuclear norm, and is exactly equal, when the $D$ matrix is equal to the diagonal matrix, to the nuclear norm, which ingeniously avoids the calculation of the singular value of the matrix. To the best of our knowledge, there is no literature to generalize and apply it to solve tensor complete problems. Inspired by this, in this paper we propose a class of tensor minimization model based on $L_{2,1}$ norm and CSVD-QR method for the tensor complete problem, which is convex and therefore has a global minimum solution.