Tensor Full Feature Measure and Its Nonconvex Relaxation Applications to Tensor Recovery
Paper and Code
Sep 25, 2021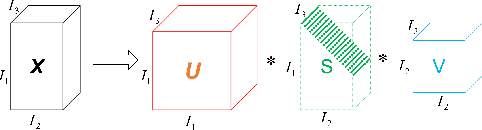
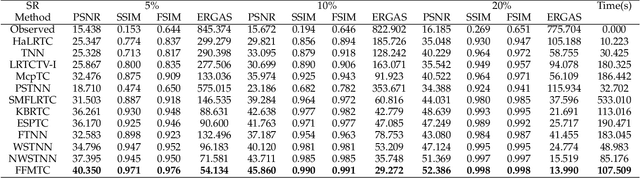


Tensor sparse modeling as a promising approach, in the whole of science and engineering has been a huge success. As is known to all, various data in practical application are often generated by multiple factors, so the use of tensors to represent the data containing the internal structure of multiple factors came into being. However, different from the matrix case, constructing reasonable sparse measure of tensor is a relatively difficult and very important task. Therefore, in this paper, we propose a new tensor sparsity measure called Tensor Full Feature Measure (FFM). It can simultaneously describe the feature information of each dimension of the tensor and the related features between two dimensions, and connect the Tucker rank with the tensor tube rank. This measurement method can describe the sparse features of the tensor more comprehensively. On this basis, we establish its non-convex relaxation, and apply FFM to low rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA). LRTC and TRPCA models based on FFM are proposed, and two efficient Alternating Direction Multiplier Method (ADMM) algorithms are developed to solve the proposed model. A variety of real numerical experiments substantiate the superiority of the proposed methods beyond state-of-the-arts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge