Tensor Recovery Based on Tensor Equivalent Minimax-Concave Penalty

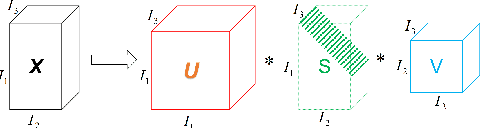
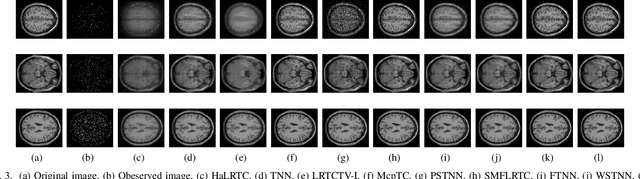
Tensor recovery is an important problem in computer vision and machine learning. It usually uses the convex relaxation of tensor rank and $l_{0}$ norm, i.e., the nuclear norm and $l_{1}$ norm respectively, to solve the problem. It is well known that convex approximations produce biased estimators. In order to overcome this problem, a corresponding non-convex regularizer has been proposed to solve it. Inspired by matrix equivalent Minimax-Concave Penalty (EMCP), we propose and prove theorems of tensor equivalent Minimax-Concave Penalty (TEMCP). The tensor equivalent MCP (TEMCP) as a non-convex regularizer and the equivalent weighted tensor $\gamma$ norm (EWTGN) which can represent the low-rank part are obtained. Both of them can realize weight adaptive. At the same time, we propose two corresponding adaptive models for two classical tensor recovery problems, low-rank tensor completion (LRTC) and tensor robust principal component analysis (TRPCA), and the optimization algorithm is based on alternating direction multiplier (ADMM). This novel iterative adaptive algorithm can produce more accurate tensor recovery effect. For the tensor completion model, multispectral image (MSI), magnetic resonance imaging (MRI) and color video (CV) data sets are considered, while for the tensor robust principal component analysis model, hyperspectral image (HSI) denoising under gaussian noise plus salt and pepper noise is considered. The proposed algorithm is superior to the state-of-arts method, and the algorithm is guaranteed to meet the reduction and convergence through experiments.