Going Beyond Linear Mode Connectivity: The Layerwise Linear Feature Connectivity

Recent work has revealed many intriguing empirical phenomena in neural network training, despite the poorly understood and highly complex loss landscapes and training dynamics. One of these phenomena, Linear Mode Connectivity (LMC), has gained considerable attention due to the intriguing observation that different solutions can be connected by a linear path in the parameter space while maintaining near-constant training and test losses. In this work, we introduce a stronger notion of linear connectivity, Layerwise Linear Feature Connectivity (LLFC), which says that the feature maps of every layer in different trained networks are also linearly connected. We provide comprehensive empirical evidence for LLFC across a wide range of settings, demonstrating that whenever two trained networks satisfy LMC (via either spawning or permutation methods), they also satisfy LLFC in nearly all the layers. Furthermore, we delve deeper into the underlying factors contributing to LLFC, which reveal new insights into the spawning and permutation approaches. The study of LLFC transcends and advances our understanding of LMC by adopting a feature-learning perspective.

Detecting Rotated Objects as Gaussian Distributions and Its 3-D Generalization

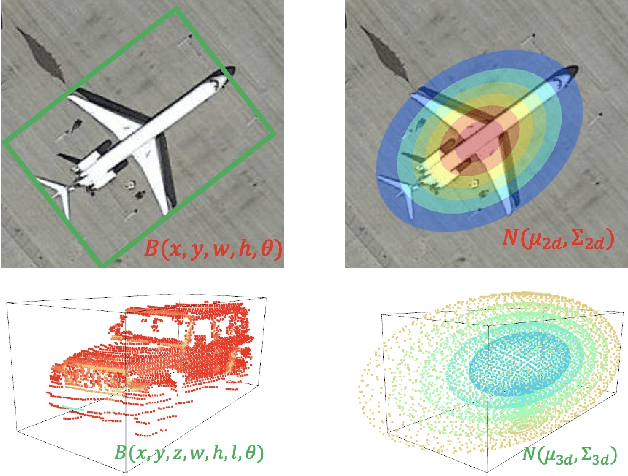
Existing detection methods commonly use a parameterized bounding box (BBox) to model and detect (horizontal) objects and an additional rotation angle parameter is used for rotated objects. We argue that such a mechanism has fundamental limitations in building an effective regression loss for rotation detection, especially for high-precision detection with high IoU (e.g. 0.75). Instead, we propose to model the rotated objects as Gaussian distributions. A direct advantage is that our new regression loss regarding the distance between two Gaussians e.g. Kullback-Leibler Divergence (KLD), can well align the actual detection performance metric, which is not well addressed in existing methods. Moreover, the two bottlenecks i.e. boundary discontinuity and square-like problem also disappear. We also propose an efficient Gaussian metric-based label assignment strategy to further boost the performance. Interestingly, by analyzing the BBox parameters' gradients under our Gaussian-based KLD loss, we show that these parameters are dynamically updated with interpretable physical meaning, which help explain the effectiveness of our approach, especially for high-precision detection. We extend our approach from 2-D to 3-D with a tailored algorithm design to handle the heading estimation, and experimental results on twelve public datasets (2-D/3-D, aerial/text/face images) with various base detectors show its superiority.

Learning High-Precision Bounding Box for Rotated Object Detection via Kullback-Leibler Divergence

Existing rotated object detectors are mostly inherited from the horizontal detection paradigm, as the latter has evolved into a well-developed area. However, these detectors are difficult to perform prominently in high-precision detection due to the limitation of current regression loss design, especially for objects with large aspect ratios. Taking the perspective that horizontal detection is a special case for rotated object detection, in this paper, we are motivated to change the design of rotation regression loss from induction paradigm to deduction methodology, in terms of the relation between rotation and horizontal detection. We show that one essential challenge is how to modulate the coupled parameters in the rotation regression loss, as such the estimated parameters can influence to each other during the dynamic joint optimization, in an adaptive and synergetic way. Specifically, we first convert the rotated bounding box into a 2-D Gaussian distribution, and then calculate the Kullback-Leibler Divergence (KLD) between the Gaussian distributions as the regression loss. By analyzing the gradient of each parameter, we show that KLD (and its derivatives) can dynamically adjust the parameter gradients according to the characteristics of the object. It will adjust the importance (gradient weight) of the angle parameter according to the aspect ratio. This mechanism can be vital for high-precision detection as a slight angle error would cause a serious accuracy drop for large aspect ratios objects. More importantly, we have proved that KLD is scale invariant. We further show that the KLD loss can be degenerated into the popular $l_{n}$-norm loss for horizontal detection. Experimental results on seven datasets using different detectors show its consistent superiority, and codes are available at https://github.com/yangxue0827/RotationDetection.

Bridging Disentanglement with Independence and Conditional Independence via Mutual Information for Representation Learning

Existing works on disentangled representation learning usually lie on a common assumption: all factors in disentangled representations should be independent. This assumption is about the inner property of disentangled representations, while ignoring their relation with external data. To tackle this problem, we propose another assumption to establish an important relation between data and its disentangled representations via mutual information: the mutual information between each factor of disentangled representations and data should be invariant to other factors. We formulate this assumption into mathematical equations, and theoretically bridge it with independence and conditional independence of factors. Meanwhile, we show that conditional independence is satisfied in encoders of VAEs due to factorized noise in reparameterization. To highlight the importance of our proposed assumption, we show in experiments that violating the assumption leads to dramatic decline of disentanglement. Based on this assumption, we further propose to split the deeper layers in encoder to ensure parameters in these layers are not shared for different factors. The proposed encoder, called Split Encoder, can be applied into models that penalize total correlation, and shows significant improvement in unsupervised learning of disentangled representations and reconstructions.